To solve some problems, the table of trigonometric identities will be useful, which will make it much easier to perform the transformation of functions:

Elementary trigonometric identities

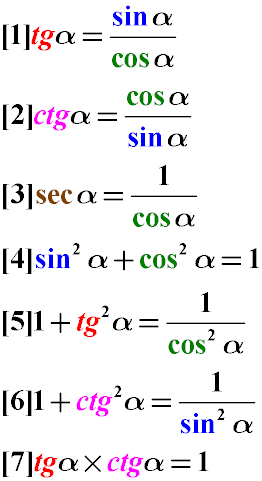
The quotient of the sine of the alpha angle by the cosine of the same angle is equal to the tangent of this angle (Formula 1). See also the proof of the correctness of the transformation of the simplest trigonometric identities.
The quotient of the cosine of the angle α to the sine of the same angle is equal to the cotangent of the same angle (Formula 2)
The angle of the angle is equal to one divided by the cosine of the same angle (Formula 3)
The sum of the squares of the sine and cosine of the same angle is one (Formula 4). see also the proof of the sum of the squares of the cosine and the sine.
The sum of the unit and the tangent of the angle is equal to the ratio of one to the square of the cosine of this angle (Formula 5)
The unit plus the cotangent of the angle is equal to the quotient of the unit divided by the sine square of this angle (Formula 6)
The product of the tangent per cotangent of the same angle is one (Formula 7).

Transformation of the negative angles of trigonometric functions (parity and oddness)

In order to get rid of the negative value of the degree angle measure in calculating the sine, cosine or tangent, we can use the following trigonometric transformations (identities), based on the principles of parity or odd trigonometric functions.

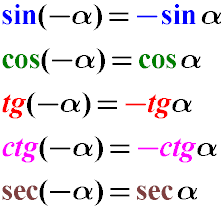
As you can see, the cosine and secant is an even function, the sine, tangent and cotangent are odd functions.

The sine of the negative angle is equal to the negative value of the sine of the same positive angle (minus the sine alpha).
The cosine of "minus alpha" will give the same value as the cosine of the alpha angle.
Tangent minus alpha is equal to minus tangent alpha.

Formulas for the reduction of the double angle (sine, cosine, tangent and cotangent of the double angle)

If it is necessary to divide the angle in half, or vice versa, go from a double angle to a single angle, we can use the following trigonometric identities:

 

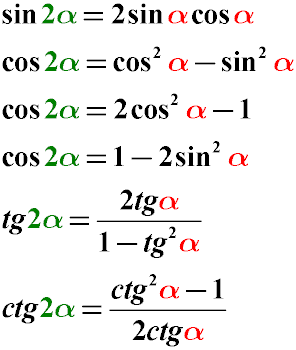
The transformation of the double angle (the sine of the double angle, the cosine of the double angle and the tangent of the double angle) into the single angle occurs according to the following rules:

The sine of the double angle is equal to twice the product of the sine by the cosine of the single angle

The cosine of the double angle is equal to the difference of the square of the cosine of the single angle and the square of the sine of this angle

The cosine of the double angle is equal to twice the square of the cosine of the single angle minus one

The cosine of the double angle is one minus the double sine square of the single angle

The tangent of a double angle is equal to a fraction whose numerator is the double tangent of a single angle, and the denominator is equal to one minus the tangent of the square of a single angle.

The cotangent of the double angle is equal to a fraction whose numerator is the square of the cotangent of a single angle minus one, and the denominator is twice the cotangent of the single angle

Universal Trigonometric Substitution Formulas

The following transformation formulas can be useful when you need to split the argument of the trigonometric function (sin α, cos α, tg α) into two and bring the expression to half the angle. From the value of α we obtain α / 2.

These formulas are called the formulas of the universal trigonometric substitution. Their value lies in the fact that the trigonometric expression with their help reduces to the expression of the half-angle tangent, regardless of which trigonometric functions (sin cos tg ctg) were in the expression initially. After this, the equation with a half-angle tangent is much easier to solve.

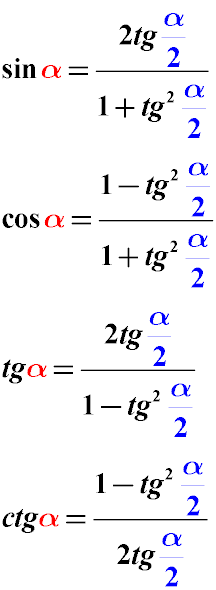
Trigonometric identities of the half-angle transformation

The formulas for trigonometric transformation of the half-value of the angle to its integral value are shown below.
The value of the argument of the trigonometric function α / 2 is reduced to the value of the argument of the trigonometric function α.

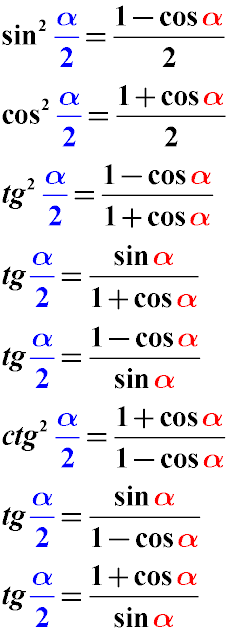
Trigonometric formulas for adding angles

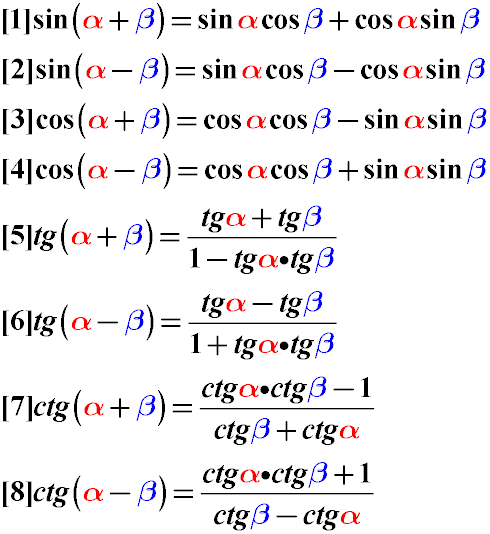
cos (α - β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α - β) = sin α · cos β - sin β · cos α 
cos (α + β) = cos α · cos β - sin α · sin β 

The tangent and cotangent sum of the alpha and beta angles can be transformed according to the following rules for converting trigonometric functions:

The tangent of the sum of the angles is equal to a fraction whose numerator is the sum of the tangent of the first and tangent of the second angle, and the denominator is one minus the product of the tangent of the first angle by the tangent of the second angle.

The tangent of the difference in angles is equal to a fraction whose numerator is equal to the difference between the tangent of the reduced angle and the tangent of the subtrahend angle, and the denominator to unity plus the product of the tangents of these angles.

The cotangent of the sum of angles is equal to a fraction whose numerator is equal to the product of the cotangents of these angles plus one, and the denominator is equal to the difference between the cotangent of the second angle and the cotangent of the first angle.

The cotangent of the difference of angles is equal to a fraction whose numerator is the product of cotangents of these angles minus one, and the denominator is equal to the sum of the cotangents of these angles.

These trigonometric identities are useful when you need to calculate, for example, the tangent of 105 degrees (tg 105). If it is represented as tg (45 + 60), then we can use the above identity transformations of the tangent of the sum of the angles, after which we just substitute the tabulated values of tangent 45 and tangent 60 degrees.

Formulas for the transformation of a sum or difference of trigonometric functions

Expressions representing a sum of the form sin α + sin β can be transformed using the following formulas:

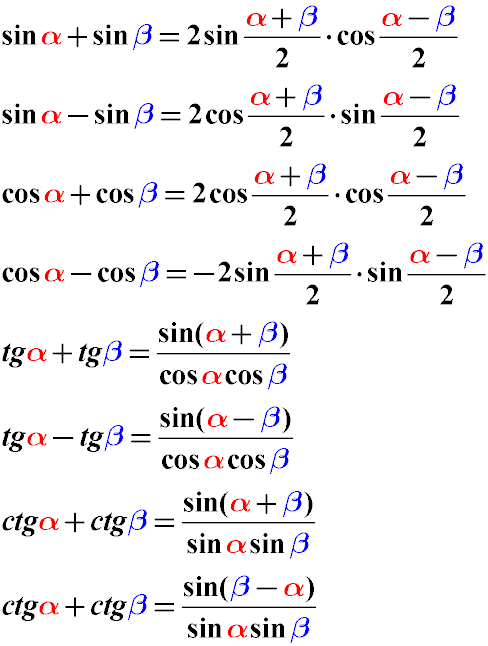
The triple-angle formulas are the transformation of sin3α cos3α tg3α into sinα cosα tgα

Sometimes it is necessary to transform the triple value of the angle so that the angle of α becomes the argument of the trigonometric function instead of 3α.
In this case, we can use the formulas (identities) of the transformation of the triple angle:

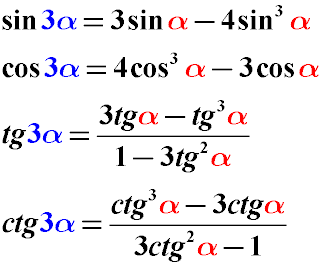
The transformation formulas for a product of trigonometric functions

If there is a need to convert the product of sines of different angles of cosines of different angles or even the product of the sine to the cosine, then we can use the following trigonometric identities:

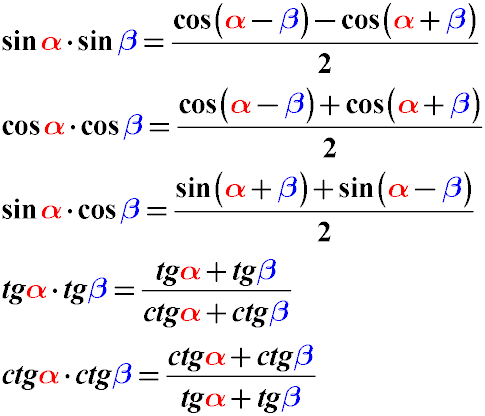
In this case, the product of the sine, cosine or tangent functions of different angles will be converted into a sum or a difference.

The formulas for reducing trigonometric functions

Use the reduction table as follows. In the line, select the function that interests us. In the column there is an angle. For example, the sine of the angle (α + 90) at the intersection of the first row and the first column, we clarify that sin (α + 90) = cos α.

See also the complete list of formulas for reducing trigonometric functions.

Angle	α + 90  α + π/2	α + 180  α + π	α + 270  α + 3π/2	90 - α  π/2- α	180 - α  π- α	270 - α  3π/2- α	360 - α  2π- α
sin	cos α	-sin α	-cos α	cos α	sin α	-cos α	-sin α
cos	-sin α	-cos α	sin α	sin α	-cos α	-sin α	cos α
tg	-ctg α	tg α	-ctg α	ctg α	-tg α	ctg α	-tg α
ctg	-tg α	ctg α	-tg α	tg α	-ctg α	tg α	-ctg α