Свойства длин сторон четырехугольника

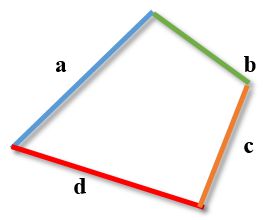
Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

|a -b| ≤ c + d

|a -c| ≤ b + d

|a -d| ≤ b + c

|b -c| ≤ a + d

|b -d| ≤ a + b

|c -d| ≤ a + b

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.

a ≤ b + c + d

b ≤ a + c + d

c ≤ a + b + d

d ≤ a + b + c

Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (<). Равенство достигается только в случае,
если четырехугольник является "вырожденным", то есть три его точки лежат на одной прямой. То есть эта ситуация не попадает под
классическое определение четырехугольника.

Задачи о возможности существования четырехугольника с заданными сторонами

Задача.

Существует ли четырехугольник, если дл:ины сторон 1 см, 3 см, 5 см, 9 см?

Решение.

Для того, чтобы четырехугольник существовал, необходимо, чтобы длина одной из его сторон была меньше, чем сумма длин трех остальных сторон,
иначе будет невозможно замкнуть периметр.

Для проверки возьмем наибольшую из сторон (9 см). Тогда сумма остальных составит 1+3+5 = 9 см. Это означает, что длины этих сторон либо
должны быть отложены как часть отрезка (9 см) большей стороны, либо такую фигуру замкнуть невозможно.
Вывод: такой четырехугольник существовать не может.

Ответ: Нет не существует.

Задача.

Существует ли четырехугольник, если дл:ины сторон 5 см, 17 см, 3 см, 7 см?

Решение.

Для того, чтобы четырехугольник существовал, необходимо, чтобы длина одной из его сторон была меньше, чем сумма длин трех остальных сторон,
иначе будет невозможно замкнуть периметр.

Для проверки возьмем наибольшую из сторон (17 см). Тогда сумма остальных составит 7+3+5 = 15 см. Это означает, что такую фигуру замкнуть
 невозможно. Вывод: такой четырехугольник существовать не может.

Ответ: Нет не существует.