Discrete random variables are variables that can take on only specific, separate values. For example, the number of points rolled on a die or
the number of students in a class (we know the list of all student groups, but we don't know which group is currently in session). Another example
could be the number of available parking spaces (all possible states of the parking lot are known). These values can be listed and have a finite or
countable set of possible values.

Main Characteristics of Discrete Random Variables:

1. Probability Distribution: Determines the probability of each possible value of the random variable.
2. Expected Value (Mean): The average value of all possible values of the random variable, weighted by their probabilities.
3. Variance: A measure of the spread of the values of the random variable relative to its expected value.
4. Distribution Function: A function that shows the probability that the random variable will take a value less than or equal to a given value.

Example 1: Rolling a Die

Let X be a discrete random variable representing the number of points rolled on a die. Possible values of X: 1, 2, 3, 4, 5, 6.
The probability of each value is 1/6.

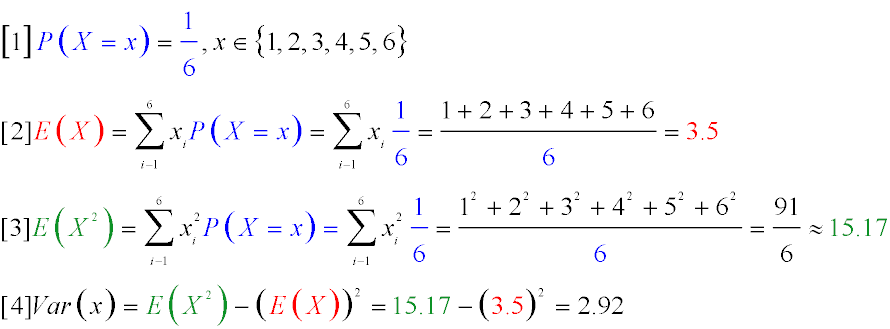
Probability Distribution: An equally likely event (1/6) of rolling one of the six predetermined values. (Formula 1)

Expected Value (Mean): The sum of the values of each face of the die, multiplied by the probability of rolling them. (Formula 2)

Expected Value of the Square of the Random Variable X (E(X²)): It is calculated as the sum of the products of the squares of the possible values
of the random variable and their probabilities. (Formula 3)

Variance: (Formula 4)