Список предметов
Problem. The probability distribution of the discrete random variable
5 / 7

Problem

The probability distribution of the discrete random variable X is given in the table:


xi 27 77 85 91 98
pi 0.2 0.4 0.1 0.2 0.1

Find:

  1. The expected value M(X)
  2. The variance D(X)
  3. The standard deviation σ(X)
  4. Construct the probability distribution polygon.

Solution

1. Expected Value M(X)

The expected value M(X) is the sum of the products of xi and pi:

M(X) = ∑xipi = 27⋅0.2 + 77⋅0.4 + 85⋅0.1 + 91⋅0.2 + 98⋅0.1 = 72.7

2. Variance D(X)

To determine the variance, we first construct the table of squared deviations from the expected value [xi−M(X)]2.
For x1, the value [xi−M(X)]2 = (27−72.7)2 = 2088.49. The other values are given in the table:


[xi - M(X)]2 2088.49 18.49 151.29 334.89 640.09
pi 0.2 0.4 0.1 0.2 0.1

Now, we determine the variance D(X) as the sum of the products [xi−M(X)]2pi:

D(X) = ∑i[xi−M(X)]2pi = 2088.49⋅0.2 + 18.49⋅0.4 + 151.29⋅0.1 + 334.89⋅0.2 + 640.09⋅0.1 = 571.21

3. Standard Deviation σ(X)

The standard deviation σ(X) is the square root of the variance:

σ(X) = D(X) = 571.21 = 23.9

4. Probability Distribution Polygon

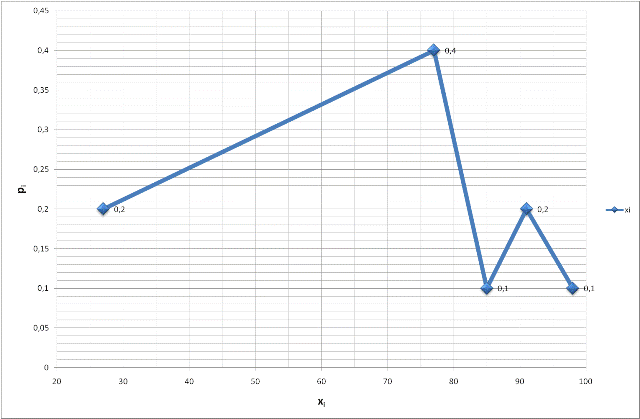
To construct the probability distribution polygon, plot the points (xi,pi) on a graph and connect them with straight lines. Here are the points:

  • (27, 0.2)
  • (77, 0.4)
  • (85, 0.1)
  • (91, 0.2)
  • (98, 0.1)

This polygon visually represents the probability distribution of the discrete random variable X.

Полигон распределения дискретной случайной величины



 Discrete Random Variables | Описание курса | Mathematical statistics