Statics

Basic Concepts, Laws, and Formulas

Statics is a branch of mechanics that studies the conditions of equilibrium of rigid bodies.

Equilibrium is the state of a body in which it is at rest, moves in a straight line, or rotates uniformly around some fixed axis passing through the center
of mass of the body.

In elementary physics, the statics of a material point and some aspects of the statics of a rigid body are studied.

Relative rest and motion of a material point at a constant speed can be considered as a special case of variable motion, in which its acceleration is zero.
According to the basic equation of dynamics, a = 0 and v=const, if:

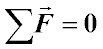
Condition of Static Position of a Body

This is the condition of equilibrium. For the equilibrium of a material point, it is necessary that the geometric sum of all forces applied to the point is zero.
The condition of equilibrium can be written differently. For this, all forces acting on the material point need to be projected onto any two axes (usually
perpendicular axes Ox and Oy) and the sums of the projections of the forces on these axes should be set to zero:

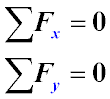
Equilibrium of a Body in a Plane Two-Dimensional Coordinate System

These equations are called the equilibrium equations of a material point in projections.

The equilibrium of a rigid body depends not only on the magnitude and direction of the acting forces but also on where they are applied. The mechanical
state of an absolutely rigid body does not change if the point of application of the force acting on it is moved along the line of its action.

The resultant of two or more forces acting on a body along one line or applied to the body at an angle to each other is equal to their vector sum and is
found by the parallelogram rule.

Two parallel forces can be balanced by one force. The balancing force is parallel to them, and its magnitude is equal to the algebraic sum of the
magnitudes of the component forces: F=F₁±F₂. The "plus" sign is taken when the forces are directed in the same direction, the "minus"
sign - in opposite directions.

The measure of the interaction of bodies, during which deformation or change in the angular velocity of rotation of bodies occurs, is the moment of force.

The magnitude of the moment of force relative to some point O is equal to the product of the magnitude of the force and the length of the perpendicular
l (arm), dropped from point O to the line of action of the force: M=Fl.

The moment of force, which tends to turn the body relative to point O in the direction of clockwise rotation, is taken with a "plus" sign, counterclockwise
- with a "minus" sign. If several forces act on the body, located in one plane (a plane system of forces), the magnitude of the resultant moment of these
forces relative to the chosen point OO is equal to the algebraic sum of the individual moments:

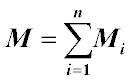
Resultant Moment of Force

The resultant moment of force is equal to the sum of the moments of individual forces.

A system of two equal antiparallel forces acting on a body not along one line is called a couple of forces. Relative to any point belonging to the plane of
the forces, the couple of forces creates the same rotating moment M=Fl, where F is the magnitude of one of the forces, l is the shortest distance between
their lines of action (arm of the couple).

If several forces act on a body lying in one plane, and the body is in a state of rest or uniform motion (translational or rotational around an axis passing
through the center of mass of the body), the geometric sum of the applied forces and the algebraic sum of the moments, taken relative to an arbitrary point,
must be zero.

Conditions of Equilibrium of a Body or System of Bodies

These conditions of equilibrium of a body or system of bodies include:

1. The geometric sum of all forces applied to the body must be zero:
2. The algebraic sum of the moments of all forces relative to any point must be zero:

These two conditions ensure both translational and rotational equilibrium of the body. It is important to note that for complex systems of bodies consisting
of several interconnected elements, the conditions of equilibrium must be met for each element of the system separately.

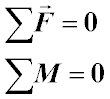
Examples of Applications of Statics

Statics finds wide application in various fields of science and technology. For example, in construction and architecture, statics is used to calculate the stability
of buildings and structures, determine loads on structures, and design safe and reliable engineering solutions.

In mechanical engineering, statics is used to analyze the forces and moments acting on machine parts and assemblies, which allows for the development
of efficient and durable mechanisms.

In biomechanics, statics is used to study the equilibrium and stability of the human body, analyze movements, and develop orthopedic devices and prostheses.

Thus, statics is an important branch of mechanics that allows solving many practical problems related to the equilibrium and stability of various objects
and systems.