Дискретні випадкові величини — це величини, які можуть приймати тільки певні, окремі значення. Наприклад, кількість випавших очок
на гральній кості або число студентів у класі (ми знаємо список усіх груп студентів, але не знаємо, яка саме група зараз займається).
Прикладом може бути кількість вільних місць на стоянці (відомі всі можливі варіанти стану стоянки). Ці значення можуть бути перераховані
і мають кінцеву або зліченну множину можливих значень.

Основні характеристики дискретних випадкових величин:

1. Розподіл ймовірностей: Визначає ймовірність кожного можливого значення випадкової величини.
2. Математичне сподівання (середнє значення): Середнє значення всіх можливих значень випадкової величини, зважене за їх ймовірностями.
3. Дисперсія: Міра розкиду значень випадкової величини відносно її математичного сподівання.
4. Функція розподілу: Функція, яка показує ймовірність того, що випадкова величина прийме значення, менше або рівне заданому.

Приклад 1: Гральна кістка

Нехай X — дискретна випадкова величина, що представляє кількість випавших очок на гральній кості.
Можливі значення X: 1, 2, 3, 4, 5, 6. Ймовірність кожного значення дорівнює 1/6.

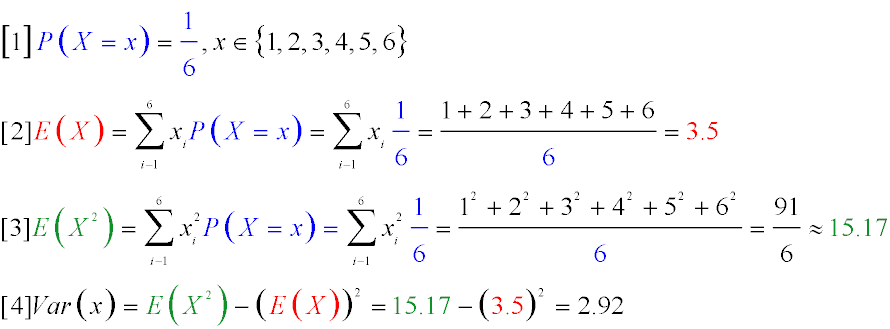
Розподіл ймовірностей: Формула 1

Математичне очікування (середнє значення): Формула 2

E(X²) - це математичне очікування квадрата випадкової величини X. Воно обчислюється як сума добутків квадратів можливих значень
випадкової величини з їхньої ймовірності. Формула 3

Дисперсія: Формула 4