Розподіл ймовірностей дискретної випадкової величини

Задача

Закон розподілу дискретної випадкової величини X задано у вигляді таблиці:

x_i	27	77	85	91	98
p_i	0.2	0.4	0.1	0.2	0.1

Знайти:

Математичне сподівання M(X)
Дисперсію D(X)
Середнє квадратичне відхилення σ(X)
Побудувати багатокутник розподілу.

Рішення

1. Математичне сподівання M(X)

Математичне сподівання M(X) дорівнює сумі добутків x_iта p_i:

M(X) = ∑x_ip_i= 27⋅0.2 + 77⋅0.4 + 85⋅0.1 + 91⋅0.2 + 98⋅0.1 = 72.7

2. Дисперсія D(X)

Для визначення дисперсії спочатку побудуємо таблицю квадратів відхилень від математичного сподівання [x_i−M(X)]².
Для x₁ значення [x_i−M(X)]²= (27−72.7)²= 2088.49. Інші значення наведені в таблиці:

[x_i - M(X)]²	2088.49	18.49	151.29	334.89	640.09
p_i	0.2	0.4	0.1	0.2	0.1

Тепер визначимо дисперсію D(X) як суму добутків [xi−M(X)]²p_i:

D(X) = ∑i[x_i−M(X)]²p_i= 2088.49⋅0.2 + 18.49⋅0.4 + 151.29⋅0.1 + 334.89⋅0.2 + 640.09⋅0.1 = 571.21

3. Середнє квадратичне відхилення σ(X)

Середнє квадратичне відхилення σ(X) дорівнює квадратному кореню з дисперсії:

σ(X) = D(X) = 571.21 = 23.9

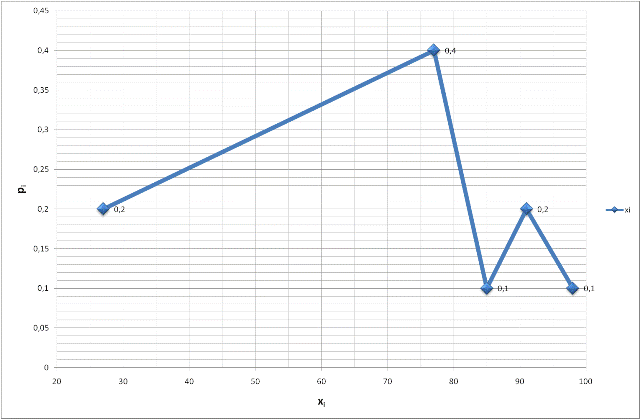
4. Багатокутник розподілу

Для побудови багатокутника розподілу, потрібно нанести точки (x_i,p_i) на графік і з'єднати їх прямими лініями. Ось точки:

(27, 0.2)
(77, 0.4)
(85, 0.1)
(91, 0.2)
(98, 0.1)

Цей багатокутник візуально представляє розподіл ймовірностей дискретної випадкової величини X.

Полигон распределения дискретной случайной величины

Дискретні випадкові величини | Описание курса | Математична статистика