|
|
Table of derivatives of trigonometric functions and inverse trigonometric functions
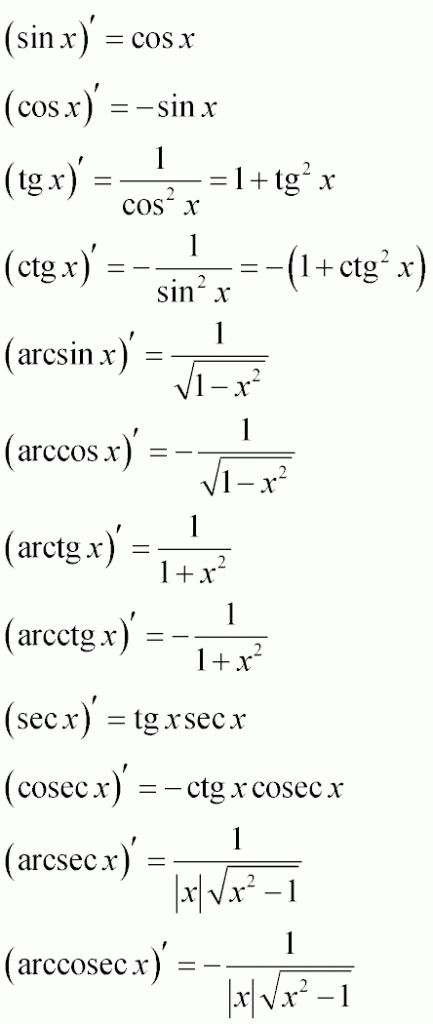
To find derivatives of trigonometric functions, the following differentiation rules are used:
- (sin x )' = cos x
The derivative of the sine of x is equal to the cosine of x
- (cos x )' = -sin x
The derivative of the cosine of x is equal to minus the sine of x
- (tg x)' = 1/ cos2x = 1 + tg2 x
The derivative of the tangent of x can be found as
- one divided by cosine squared x
- one plus tangent squared x
- (ctg x)' = - 1/ sin2x = -(1 + ctg2 x)
The derivative of the cotangent of x can be similarly represented by two expressions:
- minus one divided by sine square x
- minus the sum of one and the cotangent squared x
- (arcsin x)' = 1/(√(1-x2))
The derivative of the arcsine of x is equal to one divided by the root of the difference of one and x squared
- (arccos x)' = -1/(√(1-x2))
The derivative of the arc cosine x is equal to minus one divided by the root of the difference of one and x squared
- ( arctg x )' = 1 / ( 1 + x2 )
The derivative of the arc tangent of x is equal to a fraction whose numerator is one, and the denominator is one plus x squared
- ( arcctg x )' = -1 / ( 1 + x2 )
The derivative of the arc tangent of x is minus one divided by the sum of one and x squared
- (sex x)' = tg x sec x
The derivative of the secant of x is equal to the product of the tangent of x and the secant of x
- (cosec x)' = -ctg x cosec x
The derivative of the cosecant of x is minus the cotangent of x times the cosecant of x
- (arcsec x)' = 1 / (|x|√(x2 -1))
The derivative of the arcsecant x is equal to a fraction, in the numerator of which there is one, and in the denominator the product of
the module x and the square root of the difference x squared and one
- (arccosec x)' = - 1 / (|x|√(x2 -1))
The derivative of the arccosecant x is equal to a fraction, in the numerator of which is minus one, and in the denominator the product
of the modulus x and the root of the square difference x square and one
Derivative of the root |
Описание курса
| Derivative of logarithm
|

