Properties of Infinitesimal and Infinite Functions

For brevity, we will refer to functions as infinitesimal and infinite.

1. The algebraic sum of a finite number of infinitesimal functions is an infinitesimal function.
2. The product of an infinitesimal function and a bounded function is an infinitesimal function at a given point.
3. The product of infinitesimal functions is an infinitesimal function.
4. The sum of infinite functions of the same sign is an infinite function.
5. The product of infinite functions is an infinite function.
6. The quotient of two infinitesimal functions f₁ / f₂ is an indeterminate form of the type "0/0".
7. The difference of two infinite functions of the same sign is an indeterminate form of the type "∞-∞".
8. If f(x) as x→x₀ is an infinitesimal function, then 1 / f(x) in the same limit transition is an infinite function.

Second Definition of the Limit of a Function as x→x₀

If as x→x₀ the limit of the function f(x) is A, then the difference f(x)−A=α, where α is an infinitesimal function.

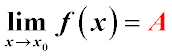
The converse statement: if as x→x₀ the function f(x) can be represented as the sum of a certain number A and an infinitesimal function,
i.e., f(x)=A+α, then the limit of the function f(x) as x→x₀ is A.

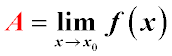
Additional Properties and Examples

1. Properties of Infinitesimal Functions:

   • If f(x) and g(x) are infinitesimal functions as x→x₀, then their sum f(x) + g(x) is also an infinitesimal function.

   • If f(x) is an infinitesimal function as x→x₀, and g(x) is a bounded function, then the product f(x)⋅g(x) is an infinitesimal function.

2. Properties of Infinite Functions:

   • If f(x) and g(x) are infinite functions as x→x₀, then their sum f(x) + g(x) is also an infinite function.

   • If f(x) is an infinite function as x→x₀, then 1 / f(x) is an infinitesimal function.

3. Examples:

   • Let f(x)=1 / x  as x→0. Then f(x) is an infinite function, and 1 / f(x)=x is an infinitesimal function.

   • Let f(x)=x² and g(x)=x³ as x→0. Then f(x) and g(x) are infinitesimal functions, and their sum f(x)+g(x)=x²+x³ as x→0
     is also an infinitesimal function.