|
|
Root derivative. Formulas for finding the derivative of the root
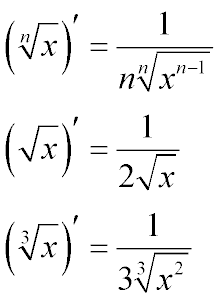
- The general case of the formula for the derivative of a root of an arbitrary degree is a fraction,
in the numerator of which there is one, and in the denominator a number equal to the degree of the root
for which the derivative was calculated, multiplied by the root of the same degree, the root expression
of which is a variable in the degree of the root for which the derivative was calculated, reduced by one
- The derivative of the square root is a special case of the previous formula.
The derivative of the square root of x is a fraction whose numerator is one and the denominator is
two times the square root of x
- The derivative of the cube root, also a special case of the general formula.
The derivative of the cube root is the one divided by the three cube roots x squared.
Below are transformations that explain why the formulas for finding the derivative of the square and cube roots
are exactly as shown in the figure.
Of course, these formulas can not be memorized at all, if we take into account that extracting the root
of a derivative degree is the same as raising a fraction to a power, the denominator of which
is equal to the same degree. Then finding the derivative of the root is reduced to applying the formula
for finding the derivative of the degree of the corresponding fraction.
Derivative of a variable under the square root
( √x )' = 1 / ( 2√x ) or 1/2 х-1/2
Explanation:
( √x )' = ( х1/2 )'
The square root is exactly the same action as raising to the power of 1/2,
which means that to find the derivative of the root,
you can apply the formula from the rule for finding the derivative of a variable to an arbitrary degree:
( х1/2 )' = 1/2 х-1/2 = 1 / (2√х)
Derivative of the cube root (derivative of the root of the third degree)
The derivative of the cube root is exactly the same as the square root.
Imagine the cube root as a power of 1/3 and find the derivative according to the general rules of differentiation.
A brief formula can be seen in the picture above, and below is an explanation of why this is so.
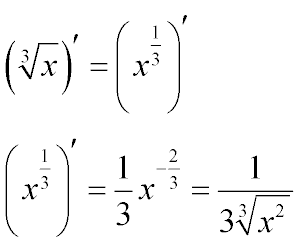
The power -2/3 is obtained by subtracting one from 1/3
Derivative of a variable under a root of an arbitrary degree
This formula is suitable for finding the derivative of the root of any degree:
( n√x )' = 1 / ( n n√xn-1 )
In a more convenient form for the eye, it is presented in the picture above.
Here:
n is the degree of the root for which the derivative is found
x - the variable for which the derivative is found
Derivative of a Number |
Описание курса
| Table of derivatives of trigonometric functions
|

