Geometric Meaning of the Derivative

DEFINITION OF THE TANGENT TO A CURVE

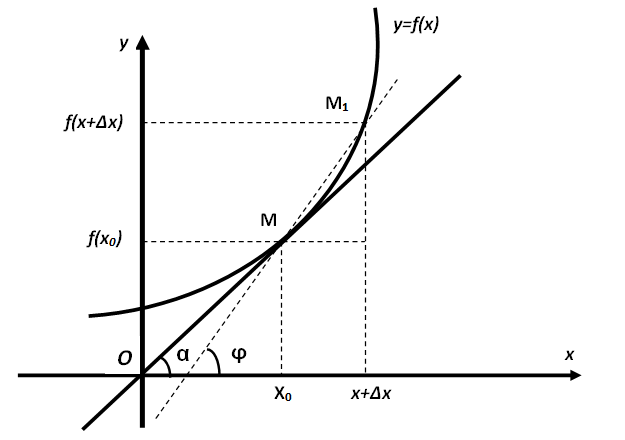
The tangent to a curve y = ƒ(x) at point M is defined as the limiting position of the secant line, drawn through point M and a neighboring point M₁ of the curve,
provided that point M₁ approaches point M along the curve indefinitely.

GEOMETRIC MEANING OF THE DERIVATIVE

The derivative of the function y = ƒ(x) at the point x₀ is numerically equal to the tangent of the angle of inclination to the O_x - axis of the tangent drawn
to the curve y = ƒ(x) at the point M(x₀,ƒ(x₀)).

In other words, the derivative indicates how sharply the function changes at a given point. If the angle of inclination of the tangent is large, the change occurs
rapidly; if the angle is small, the change is gradual.

Tangent to the curve, explaining the geometric meaning of the derivative

Practical Meaning of the Derivative

Let’s consider what the quantity found as the derivative of a function means.

First and foremost, the derivative is the rate of change of the function at a given point. It indicates how quickly the function's value changes with a small change
in the argument.

What does “rate of change” mean? Imagine the function f(x) = 5. Regardless of the value of the argument, its value remains constant. That is, the rate of change
is zero, and the derivative will also be zero:

Now, consider the function f(x) = x. The derivative is equal to one, which means: if the argument increases by one, the value of the function also increases by one.
This can be written as:

If we take the function f(x)=x², its derivative will be f'(x) = 2x. This means that the rate of change of the function depends on x: the larger x is,
the faster f(x) increases.

Second Derivative and Acceleration

If the first derivative shows the rate of change of the function, then the second derivative shows how this rate changes, that is, acceleration.

For example, consider the function f(x)=x². We already know that its first derivative is f'(x) = 2x. Let’s find the second derivative:

This means that the rate of change of the function constantly increases with the same intensity. If the second derivative is positive, the function accelerates
(the graph bends upwards); if it is negative, the function decelerates (the graph bends downwards).

Intuitive Explanation Using Motion as an Example

Imagine you're driving a car along a road. The car's speed tells you how fast you're going at any moment. Now, if you want to know how quickly
your speed is changing, you’d look at your acceleration.

A derivative in mathematics works similarly. It's like the “speed” of a function. For any given point on a curve representing the function, the derivative tells
you how fast the function's value is changing at that specific point.

Here’s an even simpler analogy:

• Function: Imagine a hill. The height of the hill at any point represents your function.

• Derivative: Now imagine you're walking up the hill. The steepness of the hill at any point (how quickly the height changes) represents the derivative.

So, if the hill is steep (the height changes quickly), the derivative is large. If the hill is flat (the height changes slowly), the derivative is small.
And if the hill is perfectly flat (no change in height), the derivative is zero.

• The derivative of the speed is acceleration: if the acceleration is positive, the car accelerates; if it is negative, the car decelerates.

• If the derivative is constant, the motion is uniform.

• If the speed changes rapidly, the derivative is large.