|
|
An ellipse is the locus of points X in the Euclidean plane for which the sum of the distances from two given points F1 and F2 (called foci) is constant,
that is, | F1X | + | F2X | = 2a.
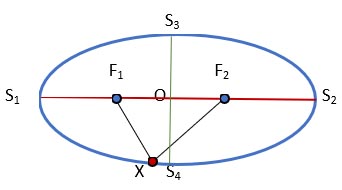
The generally accepted notations for formulas describing the properties of an ellipse are shown in the figure:
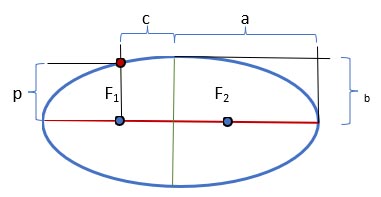
- The major axis of an ellipse is the segment passing through the foci of the ellipse, limited by the ellipse itself.
The length of the major axis is 2a
- The minor axis of an ellipse is a segment perpendicular to the major axis of the ellipse, passing through its center, and limited by the ellipse itself.
The length of the minor axis is 2b.
- The major and minor semi-axes of an ellipse (a and b) are segments drawn from the center of the ellipse to the vertices on the major and minor axes.
- Focal length (c) is the distance from the center of the ellipse to its focus..
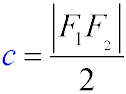
- Eccentricity (e) is the ratio of the focal length and the major semi-axis of the ellipse. It uniquely characterizes the magnitude of the "deformation"
of the ellipse in relation to the circle and is in the interval [0, 1). Closer to zero - closer to the circle.
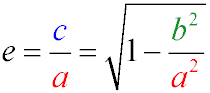
- The ellipse compression coefficient is the ratio of the lengths of the minor and major semi-axes.
When talking about the compression of an ellipse, they mean the value (1-k)
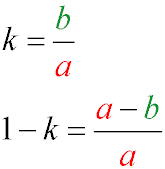
For a circle, the compression coefficient is equal to one, and the compression is zero.
- The aspect ratio and the eccentricity of the ellipse are related by the relation
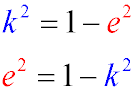
- A diameter of an ellipse is any chord that passes through its center.
A pair of diameters that have the following property are called conjugate:
the midpoints of all chords parallel to one of them are located on the second diameter.
Similarly, the midpoints of chords parallel to the second diameter lie on the first.
- The radius of an ellipse at a given point is the segment connecting the center of the ellipse with the point, as well as its length,
which is calculated using the formula
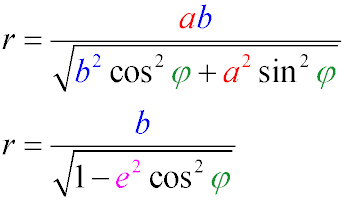
where φ is the angle between the radius and the semi-major axis.
- The focal parameter is half the length of the chord that passes through the focus of the ellipse and is perpendicular to its major axis.
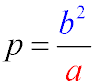
Canonical equation of an ellipse
For any ellipse, one can find a Cartesian coordinate system such that the ellipse will be described by the equation
(the canonical equation of an ellipse):
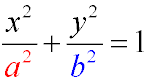
The canonical equation of an ellipse describes an ellipse with its center at the origin, whose axes coincide with the coordinate axes.
For definiteness, we assume that 0 < b ≤ a. In this case, the quantities a and b are, respectively, the major and minor semi-axes of the ellipse.
Knowing the semi-axes of the ellipse, we can calculate its focal length and eccentricity:
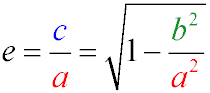
The coordinates of the foci of the ellipse in this case will be (ae;0), and (-ae;0)
The ellipse has two directrices, the equations of which can be written as x = a / ε and x = - a / ε
The equation of the diameter of an ellipse conjugate to a chord with an angular coefficient k:
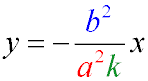
Equation of tangents of an ellipse passing through a point (x1y1)
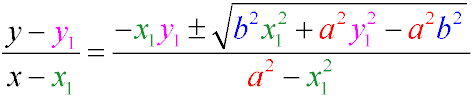
The equation of the tangents of an ellipse having a given angular coefficient k
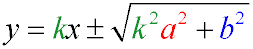
Equation of the normal of an ellipse at a point (x1y1)
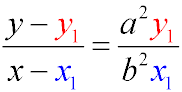
Examples of problem solving
Problem.
Find the eccentricity of the ellipse
x2 / 8 + y2 / 6 = 1
Solution.
According to the formula for finding the eccentricity of an ellipse (see above)
ε = √(64 - 36) / 8
ε = √28 / 8 = 2√7 / 8 = √7 / 4 ≈ 0,66 ≈ 2/3
Properties of Infinitesimal and Infinite Functions |
Описание курса
| Inequalities
|

