|
|
Таблиця похідних тригонометричних функцій та зворотних тригонометричних функцій
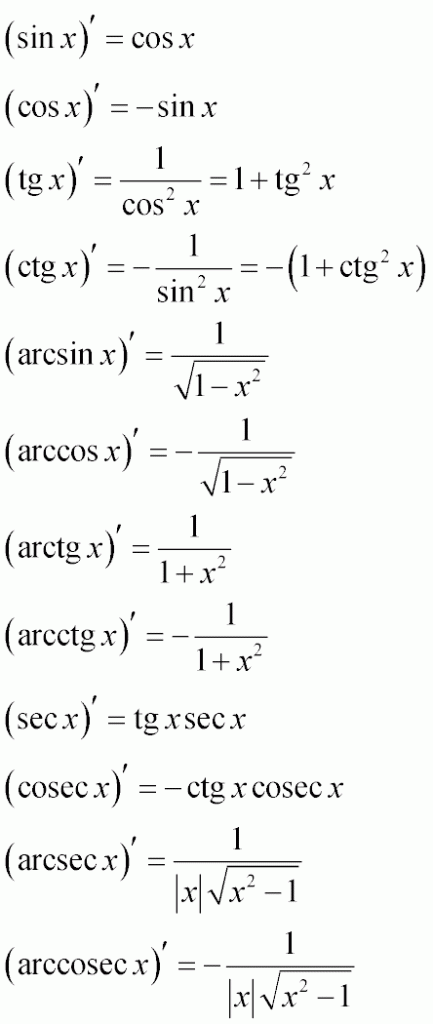
Для знаходження похідних від тригонометричних функцій застосовують такі правила диференціювання:
- (sin x )' = cos x
Похідна синуса від ікс дорівнює косінусу від ікс
- (cos x )' = -sin x
Похідна косинуса від ікс дорівнює мінус синус ікс
- (tg x)' = 1/ cos2x = 1 + tg2 x
Похідну тангенсу від ікс можна знайти як
- одиницю, поділену на косинус квадрат ікс
- одиницю плюс тангенс квадрат ікс
- (ctg x)' = - 1/ sin2x = -(1 + ctg2 x)
Похідну котангенсу від ікс, аналогічно можна уявити двома виразами:
- мінус одиницю, поділену на синус квадрат ікс
- мінус суму одиниці та котангенсу квадрат ікс
- (arcsin x)' = 1/(√(1-x2))
Похідна арксинуса ікс дорівнює одиниці, поділеній на корінь із різниці одиниці та ікс квадрат
- (arccos x)' = -1/(√(1-x2))
Похідна арккосинусу ікс дорівнює мінус одиниці, поділеній на корінь з різниці одиниці та ікс квадрат
- ( arctg x )' = 1 / ( 1 + x2 )
Похідна арктангенса від ікс дорівнює дробу, в чисельнику якого є одиниця, а в знаменнику - одиниця плюс ікс квадрат
- ( arcctg x )' = -1 / ( 1 + x2 )
Похідна арккотангенса від ікс дорівнює мінус одиниці, поділеній на суму одиниці та ікс квадрат
- (sex x)' = tg x sec x
Похідна секансу від ікс дорівнює добутку тангенсу ікс та секансу ікс
- (cosec x)' = -ctg x cosec x
Производная косеканса от икс равна минус котангенс икс умноженный на косеканс икс
- (arcsec x)' = 1 / (|x|√(x2 -1))
Похідна арксекансу ікс дорівнює дробу, в чисельнику якого одиниця, а в знаменнику добуток модуля ікс і кореня квадратного
різниці ікс квадрат і одиниці
- (arccosec x)' = - 1 / (|x|√(x2 -1))
Похідна арккосекансу ікс дорівнює дробу, в чисельнику якого мінус одиниця, а в знаменнику добуток модуля ікс і кореня
квадратного різниці ікс квадрат і одиниці
Похідна кореня |
Описание курса
| Похідна логарифма
|

