Властивості нескінченно малих і нескінченно великих функцій

Надалі для стислості будемо називати функції нескінченно малими і нескінченно великими.

1. Алгебраїчна сума кінцевого числа нескінченно малих функцій є нескінченно малою функцією.
2. Добуток нескінченно малої функції на обмежену функцію є нескінченно малою функцією в даній точці.
3. Добуток нескінченно малих функцій є нескінченно малою функцією.
4. Сума нескінченно великих функцій одного знака є нескінченно великою функцією.
5. Добуток нескінченно великих функцій є нескінченно великою функцією.
6. Частка двох нескінченно малих функцій f₁ / f₂ є невизначеністю виду «0/0».
7. Різниця двох нескінченно великих функцій одного знака є невизначеністю виду «∞-∞».
8. Якщо f(x) при x→x₀ є нескінченно малою функцією, то 1 / f(x) в тому ж граничному переході є нескінченно великою функцією.

Друге визначення границі функції при x→x₀

Якщо при x→x₀ границя функції f(x) дорівнює A, то різниця f(x)−A=α, де α – нескінченно мала функція.

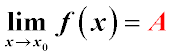
Зворотне твердження: якщо при x→x₀ функцію f(x) можна представити у вигляді суми деякого числа A і нескінченно малої функції,
тобто f(x)=A+α, то межа функції f(x) при x→x₀ дорівнює A.

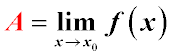
Додаткові властивості та приклади

1. Властивості нескінченно малих функцій:

   • Якщо f(x) і g(x) – нескінченно малі функції при x→x₀, то їх сума f(x)+g(x) також є нескінченно малою функцією.

   • Якщо f(x) – нескінченно мала функція при x→x₀, а g(x) – обмежена функція, то добуток f(x)⋅g(x) є нескінченно малою функцією.

2. Властивості нескінченно великих функцій:

   • Якщо f(x) і g(x) – нескінченно великі функції при x→x₀, то їх сума f(x)+g(x) також є нескінченно великою функцією.

   • Якщо f(x) – нескінченно велика функція при x→x₀, то 1 / f(x) є нескінченно малою функцією.

3. Приклади:

   • Нехай f(x)=1 / x при x→0. Тоді f(x) є нескінченно великою функцією, а 1 / f(x) = x є нескінченно малою функцією.

   • Нехай f(x)=x² і g(x)=x³ при x→0. Тоді f(x) і g(x) є нескінченно малими функціями, і їх сума f(x) + g(x) = x² + x³  при x→0
     також є нескінченно малою функцією.