|
|
Таблиця похідних простих функцій
Обчислення похідної - одна з найважливіших операцій в диференціальному обчисленні. Нижче наводиться таблиця знаходження похідних простих функцій. Більш складні правила диференціювання дивіться в інших уроках:
Наведені формули використовуйте як довідкові значення. Вони допоможуть у вирішенні диференціальних рівнянь і задач. На зображенні, в таблиці похідних простих функцій, приведена "шпаргалка" основних випадків знаходження похідної в зрозумілому для застосування вигляді, поруч з ним дано пояснення для кожного випадку.
Похідні простих функцій
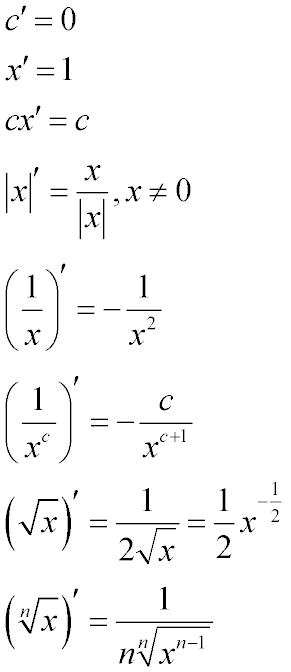 1.Похідна від числа дорівнює нулю
с'= 0
Приклад:
5'= 0
Пояснення:
Похідна показує швидкість зміни значення функції при зміні аргументу. Оскільки число не змінюється ні за яких умов - швидкість його зміни завжди дорівнює нулю.
2. Похідна змінної дорівнює одиниці
x'= 1
Пояснення:
При кожному збільшенні аргументу (х) на одиницю значення функції (результату обчислень) збільшується на цю ж саму величину. Таким чином, швидкість зміни значення функції y = x точно дорівнює швидкості зміни значення аргументу.
3. Похідна змінної і множника дорівнює цьому множнику
сx´ = с
Приклад:
(3x)´ = 3
(2x)´ = 2
Пояснення:
В даному випадку, при кожній зміні аргументу функції (х) її значення (y) зростає в с раз. Таким чином, швидкість зміни значення функції по відношенню до швидкості зміни аргументу точно дорівнює величині с.
Звідки випливає, що
(cx + b)' = c
тобто диференціал лінійної функції y = kx + b дорівнює кутовому коефіцієнту нахилу прямої (k).
4. Похідна змінної по модулю дорівнює результату ділення цієї змінної до її модулю
|x|' = x / |x| при умові, що х ≠ 0
Пояснення:
Оскільки похідна змінної (див. Формулу 2) дорівнює одиниці, то похідна модуля відрізняється лише тим, що значення швидкості зміни функції змінюється на протилежне при перетині точки початку координат (спробуйте намалювати графік функції y = | x | і переконайтеся в цьому самі. Саме таке значення і повертає вираз x / | x |. коли x <0 воно дорівнює (-1), а коли x> 0 - одиниці. тобто при негативних значеннях змінної х при кожному збільшенні зміні аргументу значення функції зменшується на точно таке ж значення, а при позитивних х - навпаки, зростає, але точно на таке ж значення.
5. Похідна змінної в ступені дорівнює добутку числа цього ступеня і змінної в ступені, зменшеної на одиницю
( xc )'= cxc-1, при умові, що xc та сxc-1,визначені, а с ≠ 0
Приклад:
(x2 )' = 2x
(x3)' = 3x2
Для запам'ятовування формули:
Знесіть ступінь змінної "вниз" як множник, а потім зменшіть саму ступінь на одиницю. Наприклад, для x2 - двійка виявилася попереду ікси, а потім зменшена ступінь (2-1 = 1) просто дала нам 2х. Те ж саме відбулося для x3 - трійку "спускаємо вниз", зменшуємо її на одиницю і замість куба маємо квадрат, тобто 3x2. Трохи "не науково", але дуже просто запам'ятати.
6. Похідна дробу 1/х
(1/х)' = - 1 / x2
Приклад:
Оскільки дріб можна представити як зведення в негативну ступінь
(1/x)' = (x-1 )' , тоді можна застосувати формулу з правила 5 таблиці похідних
(x-1 )' = -1x-2 = - 1 / х2
7. Похідна дробу зі змінною довільного ступеня в знаменнику
( 1 / xc )' = - c / xc+1
Приклад:
( 1 / x2 )' = - 2 / x3
8. Похідна кореня (похідна змінної під квадратним коренем)
( √x )' = 1 / ( 2√x ) або 1/2 х-1/2
Приклад:
( √x )' = ( х1/2 )' значить можна застосувати формулу з правила 5
( х1/2 )' = 1/2 х-1/2 = 1 / (2√х)
9. Похідна змінної під коренем довільного ступеня
( n√x )' = 1 / ( n n√xn-1 )
.
Наведена тут таблиця похідних простих функцій містить тільки основні перетворення, які (за великим рахунком) слід запам'ятати напам'ять. Знаходження більш складних похідних наведені у відповідних таблицях інших уроків:
Диференціальне числення |
Описание курса
| Похідна кореня
|
