Геометричний зміст похідної
ВИЗНАЧЕННЯ ДОТИЧНОЇ ДО КРИВОЇ
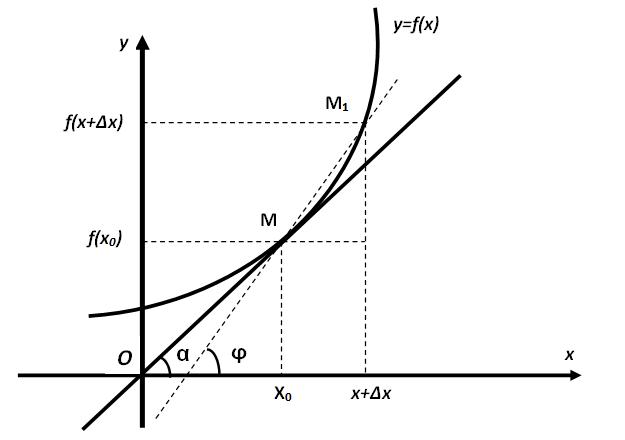
Дотичною до кривої y=ƒ(x) в точці М називається граничне положення січної, проведеної через точку М і сусідню з нею точку М1 кривої, за умови,
що точка М1 не обмежено наближається вздовж кривої до точки М.
ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ
Похідна функції y=ƒ(x) в точці х0 чисельно дорівнює тангенсу кута нахилу до осі Ох дотичної, проведеної до кривої y=ƒ(x) в точці М (х0; ƒ(x0)).
Іншими словами, похідна показує, наскільки різко змінюється функція в даній точці. Якщо кут нахилу дотичної великий, то зміна відбувається швидко,
якщо кут малий – зміна повільна.
Дотична до кривої, що пояснює геометричний зміст похідної.
Практичний зміст похідної
Розглянемо, що означає величина, знайдена нами як похідна функції.
Передусім, похідна – це швидкість зміни функції в даній точці. Вона показує, як швидко змінюється значення функції при малому зміненні аргументу.
Що таке "швидкість зміни"? Уявімо собі функцію f(x) = 5. Незалежно від значення аргументу, її значення залишається постійним.
Тобто, швидкість її зміни дорівнює нулю, а похідна також буде дорівнювати нулю:
f'(x) = 0
Тепер розглянемо функцію f(x) = x. Похідна дорівнює одиниці, що означає: якщо аргумент збільшується на одиницю, то значення функції також
збільшується на одиницю. Це можна записати так:
f'(x) = 1 Якщо ми візьмемо функцію f(x) = x², її похідна буде f'(x) = 2x. Це означає, що швидкість зміни функції залежить від x: чим більше x,
тим швидше збільшується f(x).
Друга похідна і прискорення
Якщо перша похідна показує швидкість зміни функції, то друга похідна показує, як змінюється ця швидкість, тобто прискорення.
Наприклад, розглянемо функцію f(x) = x². Ми вже знаємо, що її перша похідна дорівнює f'(x) = 2x. Знайдемо другу похідну:
f''(x) = 2 Це означає, що швидкість зміни функції постійно збільшується з однаковою інтенсивністю. Якщо друга похідна позитивна, функція прискорюється (графік вигинається вгору), якщо негативна – сповільнюється (графік вигинається вниз).
Інтуїтивне пояснення похідної на прикладі руху
Припустімо, ми їдемо на автомобілі.
-
Похідна швидкості – це прискорення: якщо прискорення позитивне, машина розганяється, якщо негативне – сповільнюється.
-
Якщо похідна постійна, рух рівномірний.
-
Якщо швидкість змінюється швидко, похідна велика.
Диференціальне числення |
Описание курса
| Таблиця похідних простих функцій
|

