Завдання. Імовірність одночасного приходу пароплавів

1. Час стоянки першого теплохода (T1): 6 годин.

2. Час стоянки другого теплохода (T2): 8 годин.

3. Загальний час доби (T): 24 години.

Час приходу обох теплоходів є незалежним і рівноможливим протягом доби. Це означає, що кожен теплохід може
прибути в будь-який момент протягом 24 годин з однаковою ймовірністю.

Для розв'язання задачі скористаємося геометричним підходом. Уявимо собі площину з осями X і Y, де X - час
приходу першого теплохода, а Y - час приходу другого теплохода. Обидві осі мають довжину 24 години.

На цій площині ми можемо побудувати квадрат розміром 24x24, де кожна точка (x, y) представляє час приходу
обох теплоходів.

Тепер розглянемо умови, за яких одному з теплоходів доведеться чекати на звільнення причалу. Це станеться,
якщо час стоянки одного теплохода перекривається з часом стоянки іншого теплохода. Тобто, якщо:

• |x - y| < 6 (перший теплохід стоїть 6 годин)

• |x - y| < 8 (другий теплохід стоїть 8 годин)

Об'єднаємо ці умови в одну: |x - y| < 6 або |x - y| < 8.

На площині це означає, що ми маємо дві смуги шириною 6 годин і 8 годин, які розташовані вздовж діагоналі
квадрата. Загальна ширина смуг, де одному з теплоходів доведеться чекати, становить 6 + 8 = 14 годин.

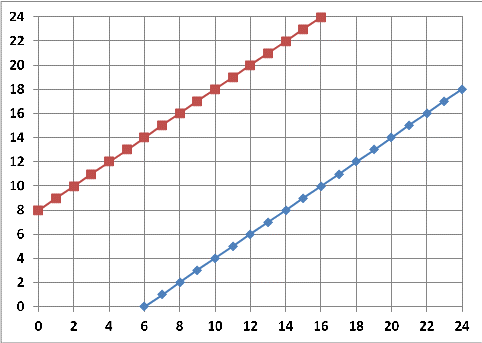
Як бачимо, час приходу одного пароплава зазначено по осі х, а другого - по осі y. Таким чином,
обидва пароплави не будуть "заважати" один одному, якщо їх час приходу (x, y) буде нижчим за
синю лінію або вище за червону.

Загальне місце варіантів приходу пароплавів, як видно з графіків, знаходиться на площині
"квадрата" зі стороною 24 години. Таким чином, відношення площі між двома лініями до загальної
площі квадрата і відображатиме ймовірність того, що одному з пароплавів доведеться чекати на
звільнення причалу під час стоянки іншого.

Шукану площу можна знайти через обчислення певного інтеграла функцій на проміжку [0;24], але
для простоти рішення ми виберемо наочніший спосіб.

Знайдемо площу трикутника обмеженого синьою лінією.

S1 = (24-6) * (24-6) / 2 = 162 (див. площу трикутника)

Тепер знайдемо площу трикутника, обмеженого червоною лінією:

S2 = (24-8) * (24-8) / 2 = 128

Загальна площа квадрата, відповідно, дорівнює 576

Площа, що геометрично відображає ймовірність настання події, що одному з пароплавів доведеться
чекати звільнення причалу під час стоянки іншого, таким чином, дорівнює:

576 – 128 – 162 = 286

Звідки ймовірність очікування звільнення причалу дорівнює:

286 / 576 = 143 / 288 ≈ 0,49653

Відповідь: 143 / 288 ≈ 0,49653