Похідна кореня. Формули для знаходження похідної кореня

Формула нахождения производной квадратного корня, кубического корня и корня произвольной степени

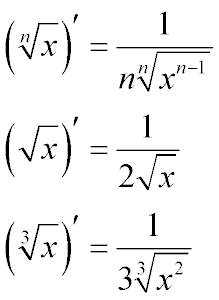
Загальний випадок формули похідної кореня довільного ступеня - дріб, у чисельнику якого одиниця,
а в знаменнику число, рівне ступеню кореня, для якого обчислювалася похідна,
помножена на корінь такого ж ступеня, підкорінний вираз якого - змінна у ступеню кореня,
для якого обчислювалася похідна , зменшена на одиницю
Похідна квадратного кореня є окремим випадком попередньої формули.
Похідна квадратного кореня з x - це дріб, чисельник якого дорівнює одиниці,
а знаменник - двійка, помножена на квадратний корінь х
Похідна кубічного кореня, також окремий випадок загальної формули.
Похідна кубічного кореня - це одиниця, поділена на три кубічні корені з ікс квадрат.

Нижче наведені перетворення, що пояснюють, чому формули знаходження похідної квадратного
та кубічного кореня саме такі, як наведені на малюнку.

Зрозуміло, дані формули можна взагалі не запам'ятовувати, якщо взяти до уваги,
що вилучення кореня похідного ступеня - це те саме, що зведення в ступінь дробу,
знаменник якого дорівнює тому ж ступеню.
Тоді знаходження похідної кореня зводиться до застосування формули
знаходження похідної ступеня відповідного дробу.

Похідна змінної під квадратним коренем

( √x )' = 1 / ( 2√x )   або 1/2 х^-1/2

Пояснення:
( √x )' = ( х^1/2 )'
Квадратний корінь - це точно та ж дія, що і зведення в ступінь 1/2,
тобто для знаходження похідної кореня можна застосувати формулу з правила
знаходження похідної від змінної довільною мірою:
( х^1/2 )' = 1/2 х^-1/2 = 1 / (2√х)

Похідна кубічного кореня (похідна кореня третього ступеня)

Похідна кубічного кореня знаходиться точно за таким самим принципом, що і квадратного.
Уявімо собі кубічний корінь як ступінь 1/3 і знайдемо похідну за загальними правилами диференціювання.
Коротку формулу можна подивитися на зображенні вище, а нижче розписано пояснення, чому саме так.
Нахождение производной кубического корня представлением через степенную функцию

Нахождение производной кубического корня представлением через степенную функцию

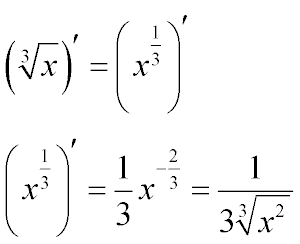
Ступінь -2/3 виходить внаслідок віднімання одиниці з 1/3

Похідна змінної під коренем довільного ступеня

Дана формула придатна для знаходження похідної кореня будь-якого ступеня:
( ⁿ√x )' = 1 / ( n ⁿ√x^n-1 )
У більш зручному для ока вигляді вона представлена на малюнку вище.
n - ступінь кореня, на якій знаходиться похідна
x - змінна, для якої знаходиться похідна

Таблиця похідних простих функцій | Описание курса | Таблиця похідних тригонометричних функцій