Problem Solving for Maximizing Profit and Sales

The local museum is visited by students and pensioners. 

The demand for student tickets is described by the equation:

P₁ = 120 - q₁ / 2

The demand for pensioners:

P₂ = 100 - q₂ / 2 

The maximum capacity of the museum is 200 people.
It is necessary to determine the price of tickets for students and pensioners to ensure the maximum occupancy of the museum and achieve the highest profit.

Comments on the Task

• In real economics, such linear demand models are rare, but within algebra, the task is reduced to finding the extremum of a function.
• The task does not account for the museum's expenses, so it is more accurate to talk about maximizing revenue rather than profit.

Step 1. Writing the Revenue Function

The solution to the task of determining the maximum revenue and the number of tickets

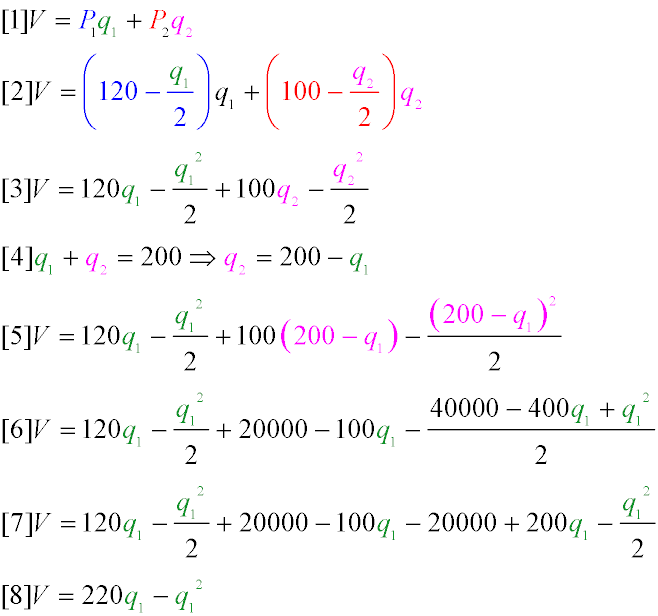
• Total revenue of the museum from ticket sales - Formula 1
• Substitute the demand equations from the problem statement - Formula 2
• Expand the brackets - Formula 3
• Now consider the museum's capacity constraint, from which we can eliminate the second variable - Formula 4
• Substitute into Formula 3 (revenue expression) the value from Formula 4 (number of visitors) to get Formula 5 with one variable.
• Expand the brackets and record the result in Formula 6.
• Simplify the expression - Formula 7
• Finally, obtain the revenue function based on the problem statement - Formula 8.

Step 2. Optimizing Revenue

As we know from algebra, a function reaches its maximum at the extremum point.
Find the extremum of the function. To do this, we need to find its derivative:

At the extremum point, the derivative of the function is zero.
Set the derivative to zero:

Now find the value of the second variable q₂:

q₂ = 200 - 110 = 90 (Formula 4)

Step 3. Determining Optimal Prices

Substitute the values into the demand equation given in the problem statement:

Step 4. Calculating Maximum Revenue

Answer: Optimal ticket prices for maximizing revenue:

• Students: 65
• Pensioners: 55
• Maximum revenue: 12,100 monetary units