|
|
Задача.
По данному статистическому распределению выборки, извлеченной из генеральной совокупности нормально распределенного признака Х построить полигон относительных частот.
Найти:
- Эмпирическую функцию распределения F(X) и построить ее график
- Несмещенные оценки генеральной средней и генеральной дисперсии D.
- Моду и медиану и размах варьирования R.
- Доверительный интервал для оценки с надежностью γ=0.95 математического ожидания α , если известно генеральное среднее квадратическое отклонение σ = 1.
| xi | -8 | -4 | 4 | 8 | 12 | 16 | 20 | 24 |
| ni | 7 | 5 | 8 | 11 | 15 | 12 | 7 | 16 |
Решение.
Эмпирическую функцию распределения представим следующим образом:
Общее количество элементов выборки 7 + 5 + 8 + 11 + 15 +12 +7 + 16 = 81
F*n(X) = {
| 0, x ≤ -8
|
7/81, x ≤ -4
|
12/81, x ≤ 4
|
20/81, x ≤ 8
|
31/81, x ≤ 12
|
| 46/81, x ≤ 16 |
58/81, x ≤ 20
|
| 63/81, x ≤ 24 |
| 1, x > 24 |
Несмещенной оценкой генеральной средней является выборочная средняя - сумма произведений xini деленная на количество элементов выборки. То есть:
x = ( (-8)*7 + (-4)*5 + 4*8 + 8*11 + 12*15 + 16*12 + 20*7 +24*16 ) / 81 = 940 / 81 ≈ 11.6049
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия (D) - сумма произведений x2ini деленная на количество элементов выборки минус М(х)2 .
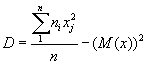
D = ( (-8)2*7 + (-4)2*5 + 42*8 + 82*11 + 122*15 + 162*12 + 202*7 +242*16 ) / 81 - 134.6746 = 18608 / 81 - 134.6746 ≈ 229.7284 - 134.6746 = 95.0538
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
S = n / (n-1) * D
S = 81 / ( 81 - 1 ) * 95.0538 ≈ 96.2420
Мода (M0) - это значение, повторяющееся в выборке с наибольшей частотой. В данном случае с наибольшей частотой (16) повторяется значение xi = 24.
То есть M0 = 24.
Медиана (Ме) - значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Ранг R (порядковый номер) медианы для упорядоченной выборки, содержащей нечетное число членов определяется как
RMe = (n + 1) / 2 = ( 81 + 1 ) / 2 = 41
То есть медиана имеет значение 12, поскольку находится в интервале элементов со значением 12, то есть 7 + 5 + 8 + 11 = 31 < Ме < 7 + 5 + 8 + 11 +15 = 46
Размах варьирования – разность между максимальной и минимальной вариантами выборки:
R = xmax - xmin
Таким образом
R = 24 - ( -8 ) = 32
Определим доверительный интервал.
Из соотношения 2Ф(t)= 0,95 (по условию задачи), откуда Ф(t) = 0,475 по таблице найдем t :
t =1,96.
σ = 1 (по условию задачи)
Точность оценки
δ = tσ / √n = 1.96 * 1 / √81 ≈ 0.2178
Доверительный интервал будет равен:
( x - δ; x + δ ), то есть ( 11.6049 - 0,2178; 11.6049 + 0,2178 )
(11,3871; 11,8227)
Генеральная и выборочная совокупность |
Описание курса
| Дисперсия альтернативного признака
|

