Дискретные случайные величины — это величины, которые могут принимать только определенные, отдельные значения. Например, количество
выпавших очков на игральной кости или число студентов в классе (мы знаем список всех групп студентов, но не знаем какая именно группа сейчас
занимается). Примером может быть количество свободных мест на стоянке (известны все возможные варианты состояния стоянки).Эти значения
могут быть перечислены и имеют конечное или счетное множество возможных значений.

Основные характеристики дискретных случайных величин:

1. Распределение вероятностей: Определяет вероятность каждого возможного значения случайной величины.
2. Математическое ожидание (среднее значение): Среднее значение всех возможных значений случайной величины,
   взвешенное по их вероятностям.
3. Дисперсия: Мера разброса значений случайной величины относительно ее математического ожидания.
4. Функция распределения: Функция, которая показывает вероятность того, что случайная величина примет значение,
   меньшее или равное заданному.

Пример 1: Игральная кость

Пусть X — дискретная случайная величина, представляющая количество выпавших очков на игральной кости.
Возможные значения X: 1, 2, 3, 4, 5, 6. Вероятность каждого значения равна 1/6.

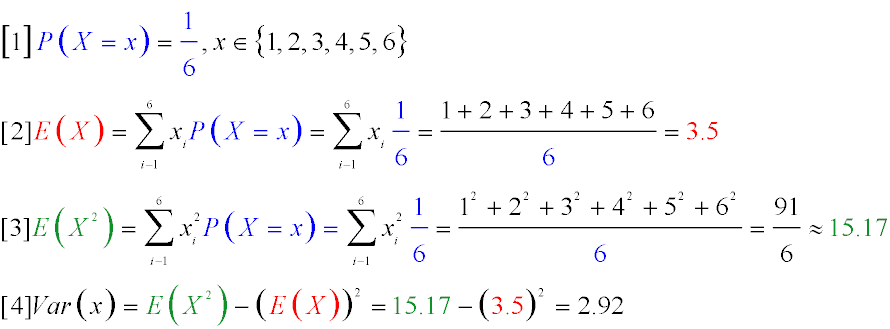
Распределение вероятностей: Формула 1

Математическое ожидание (среднее значение): Формула 2

E(X²) — это математическое ожидание квадрата случайной величины X. Оно вычисляется как сумма произведений квадратов
возможных значений случайной величины на их вероятности. Формула 3

Дисперсия: Формула 4