Цель работы – получить умения по анализу распределения данных в программе MS Excel.

Задание работы – провести анализ статистических рядов распределения с помощью надстройки “анализ данных”.

Выпишем основные формулы для расчета характеристик рядов распределения.

мода
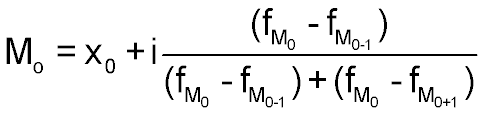медиана
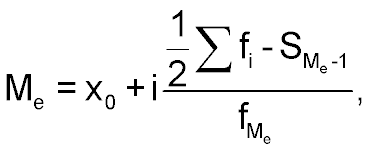дисперсия
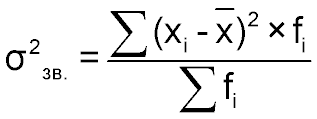Среднее квадратичное отклонение
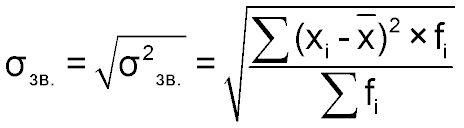Коэффициент вариации

Решать задачи по анализу рядов распределения типа в Excel можно с помощью использования программной надстройки Пакет анализа и встроенных статистических функций.

Анализ не сгруппированных статистических данных. Построим таблицу с первичными данными.

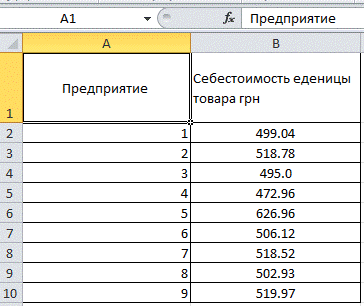
Режим Описательная статистика служит для генерации статистического отчета по основным показателям положения, рассеивания и асимметрии совокупности, которая анализируется. Для перехода в этот режим необходимо войти в меню сервис – анализ данных и выбрать этот режим. Если его нет, то его необходимо включить. Для того чтобы это сделать нужно зайти в файл-параметры-надстройки и найти там пакет анализа. Выбираем режим Описательной статистики.

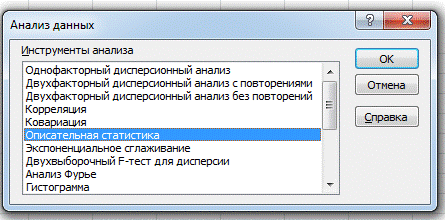
В диалоговом окне данного режима задаются следующие параметры:

1. Входной интервал – ячейки, в которых содержатся статистические данные.

2. Группирование – устанавливается положение По столбцами или По строкам в зависимости от расположения данных во входном диапазоне.

3. Метки в первом ряду – активизируется, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, то метку необходимо деактивировать. В этом случае будут автоматически созданы стандартные названия для данных выходящего диапазона.

4. Выходной интервал – в положении Выходной интервал активируется поле, в которое необходимо ввести ссылки на левую верхнюю клетку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экране появится уведомление в случае возможного наложения выходного диапазона на входные данные.

В положении Новый рабочий лист открывается новый лист, в который начиная с клетки А1 устанавливаются результаты анализа. Если нужно задать имя новому рабочему листу, который открывается, нужно ввести его имя в поле, которое расположено напротив.

В положении Новая рабочая книга открывается новая книга, на первом листе которой начиная с клетки А1 устанавливаются результаты анализа.

5. Итоговая статистика – активизируется, если в выходном диапазоне необходимо получить строку для предельной погрешности выборки при установленном уровне надежности.

6. Уровень надежности – активизируется, если в выходную таблицу необходимо включить строку для предельной погрешности при установленном уровне надежности.

7 К-тое наибольшее – активизируется, если в выходную таблицу необходимо включить строку для к-того наибольшего (начиная с максимума х_max) значения элемента совокупности. В поле напротив нужно ввести чисто к. Если к=1, то строка будет содержать максимальное значения элемента выборки.

8 К-тое наименьшее – активизируется, если в выходную таблицу необходимо включить строку для к=того наименьшего (начиная с х_min) значения элемента выборки. Введенные параметры представлены на рисунке снизу

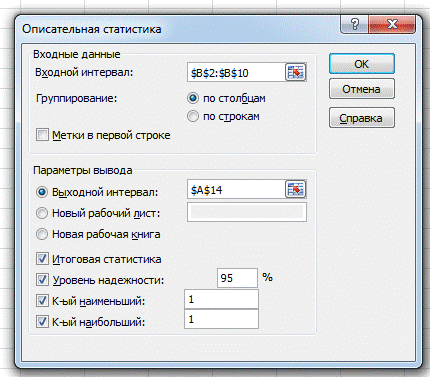
Далее на рисунке можно увидеть сам статистический отчет

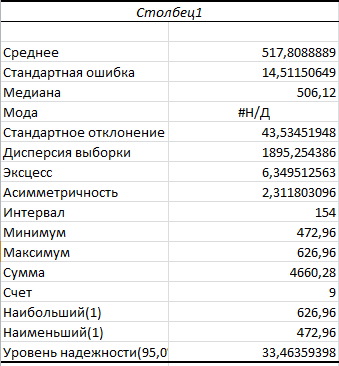
Согласно полученным данным:

Коэффициент осцилляции равен

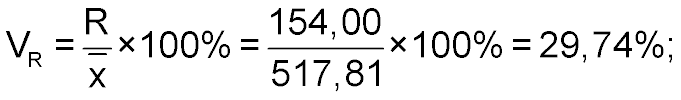
Коэффициент вариации равен

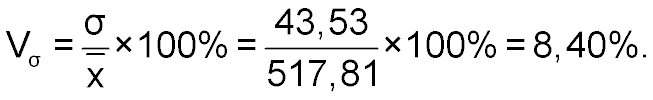
Анализ сгруппированных статистических данных

Построим таблицу с исходными данными.

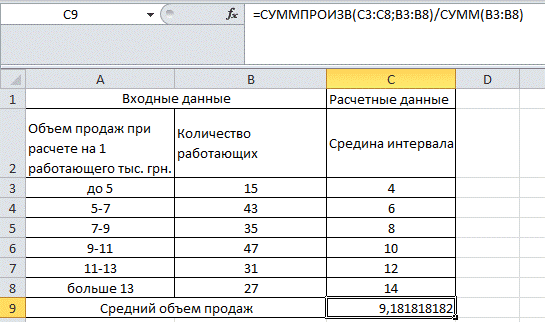
Нам нужно посчитать среднюю взвешенную арифметическую. Данная функция не представлена в Excel. Но мы можем сгруппировать несколько функций, чтобы получить нужную формулу. Используем функции СУММПРОИЗВ и СУММ. Функция СУММПРОИЗВ перемножает две группы массивов между собой и складывает полученные данные после произведения. Построим формулу =СУММПРОИЗВ(C3:C8;B3:B8)/СУММ(B3:B8)

Для вычисления моды и медианы необходимо произвести несколько расчетов

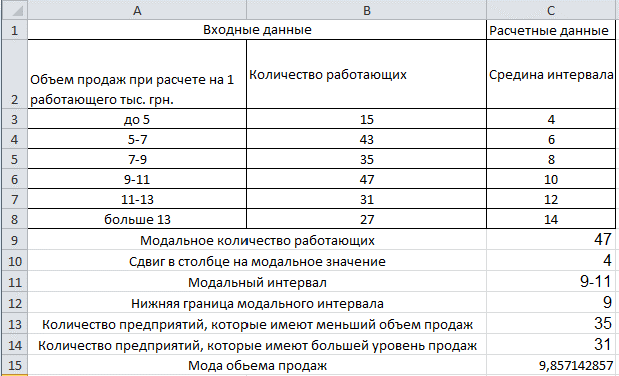
Рассчитаем модальное количество рабочих. Это можно сделать с помощью формулы =МАКС(B3:B8). Мы находим максимальное значение на выбранном диапазоне.

Найдем сдвиг в столбце на модальное значение. Это можно сделать с помощью формулы =ПОИСКПОЗ(C9;B3:B8;0). Мы находим положение нужного нам значения.

Найдем модальный интервал. Это можно сделать с помощью формулы =ИНДЕКС(A3:A8;C10;1). По заданным координатам находим значение на диапазоне.

Найдем нижнюю границу модального интервала. Сделаем это с помощью формулы =ЛЕВСИМВ(C11;1). Отделяем нужное значение от модального интервала.

Найдем количество предприятий, которые имеют меньший объем продаж. Используем формулу =ИНДЕКС(B3:B8;C10-1;1). ПО заданным координатам находим положение нужного нам значения.

Теперь найдем количество предприятий, которые имеют больший уровень продаж =ИНДЕКС(B3:B8;C10+1;1). Работает по такому же принципу.

Посчитаем моду объема продаж с помощью формулы =C12+2*((C9-C13)/((C9-C13)+(C9-C14))).

В связи с тем, что медиана делит численность ряда пополам, то она будет там, где частота составляет половину или больше половины всей суммы частот, а предыдущая накопительная частота меньше половины численности совокупности.

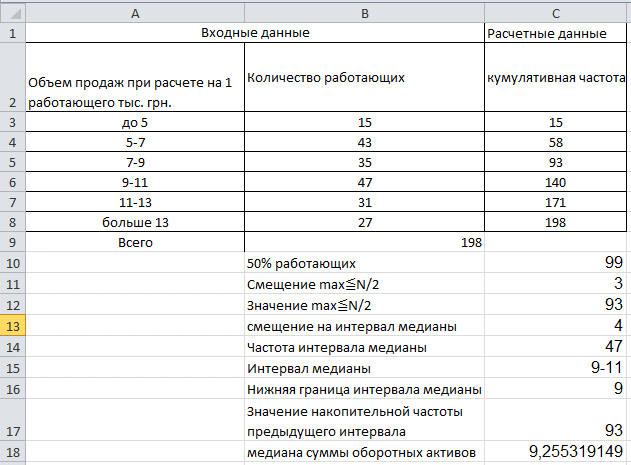
В массиве С3:С8 рассчитывается накопительная частота. Считается с помощью формулы =C3+B4 (клетка С3).

Рассчитаем общее количество рабочих с помощью формулы =СУММ(B3:B8). Мы рассчитали количество совокупности.

Найдем половину всех рабочих с помощью формулы =B9/2. Мы рассчитали половину совокупности.

Найдем смещение max≦N/2 по формуле =ПОИСКПОЗ(C10;C3:C8;1). В массиве С3:С8 рассчитывается номер позиции числа, которое является наибольшим среди чисел меньших или равных вредине интервала. Это число равно 99.

Найдем значение max≦N/2 с помощью формулы =ИНДЕКС(C3:C8;C11;1). Из числового массива С3:С8 берется число, которое удовлетворяет условиям поиска, сформированными нами в клетке С11.

Найдем смещение на интервал медианы с помощью формулы =ЕСЛИ(C10=C12;C11;C11+1).

Найдем частоту интервала медианы с помощью формулы =ИНДЕКС(B3:B8;C13;1). Формула отображает это значение.

Найдем интервал медианы по формуле =ИНДЕКС(A3:A8;C13;1). В заданном массиве находится интервал медианы.

Найдем нижнюю границу интервала по формуле =ЛЕВСИМВ(C15;1). Формула отображает нужное нам значение.

Найдем значение накопительной частоты предыдущего интервала с помощью формулы =ИНДЕКС(C3:C8;C13-1;1). В заданном интервале находится искомое значение.

Найдем медиану сумм оборотных активов с помощью формулы =C16+2*((B9/2-C17)/C14).

Расчет среднего квадратичного отклонения позволяет посчитать коэффициент вариации.

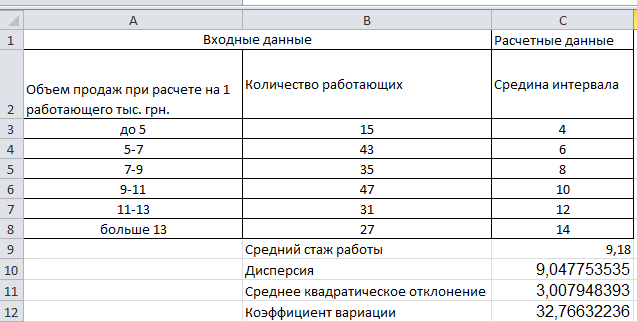
Расчет Показателей на рисунке происходит по следующим формулам:

Дисперсию мы считаем по следующей формуле

=(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;2);B3:B8))/СУММ(B3:B8).

Среднее квадратичное отклонение мы считаем по формуле

=КОРЕНЬ(C10).

Коэффициент вариации находим по формуле

=(C11/C9)*100.

Рассчитаем квартильный показатель вариации. Для этого нужно определить верхний и нижний квартили.

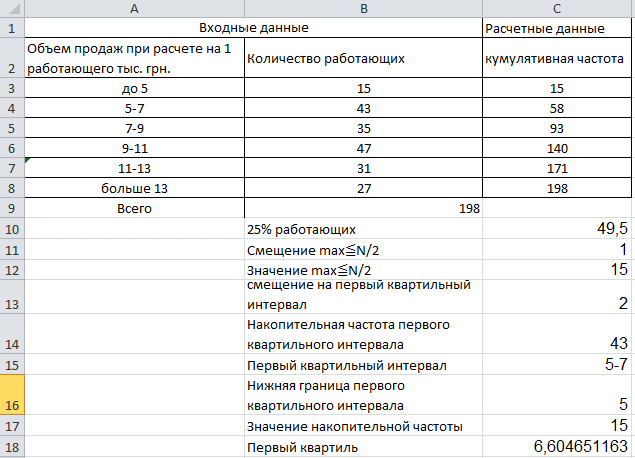
Вычисления на этом рисунке практически аналогичны расчету медианы кроме следующих пунктов:

Мы должны посчитать 25% (1/4) рабочих. Сделаем это по формуле =B9*0,25.

М должны посчитать первый квартиль. Расчет происходит по формуле =C16+2*((B9*0,25-C17)/C14).

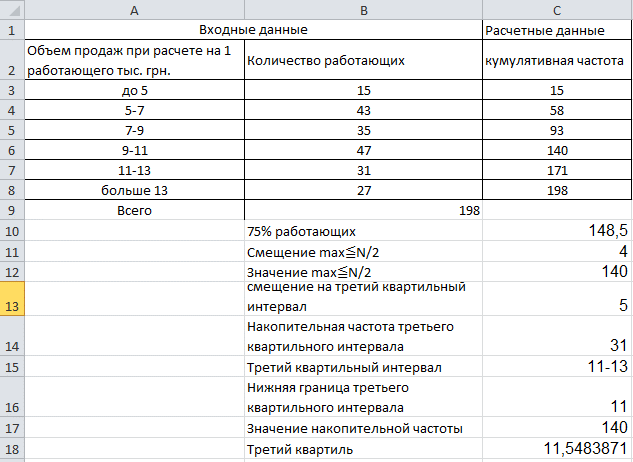
Третий квартиль находится в интервале 11-13 лет. Он равняется приблизительно 11,5. Для его вычисления мы должны поменять несколько пунктов таблицы:

Мы должны посчитать 75% рабочих. Сделаем это по формуле =B9*0,75.

Скорректируем формулу по нахождению нижней границы квартильного интервала =ЛЕВСИМВ(C15;2).

Рассчитаем третий квартиль по формуле =C16+2*((B9*0,75-C17)/C14).

Таким образом, квартильное отклонение равняется

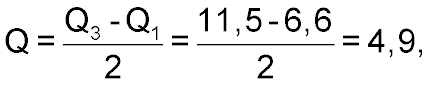
Квартильный показатель вариации равняется

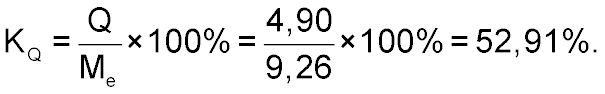
Дисперсионный анализ

Исследовалась сила влияния внешнего вида упаковки товара на покупательную способность в разных точках продажи с помощью дисперсионного анализа.

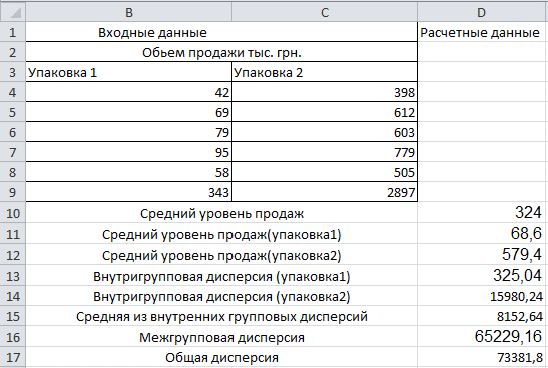
Формулы расчета:

Средний уровень продаж рассчитывается по формуле =(B9+C9)/(5+5).

Средний уровень продаж по 1 упаковке рассчитывается по формуле =B9/5.

Средний уровень продаж по 2 упаковке рассчитывается по формуле =C9/5.

Внутригрупповая дисперсия по 1 упаковке рассчитывается по формуле =ДИСПР(B4:B8).

Внутригрупповая дисперсия по 2 упаковке рассчитывается по формуле =ДИСПР(C4:C8).

Средняя из внутренних групповых дисперсий рассчитывается по формуле

=(D13×5+D14×5)/10.

Межгрупповая дисперсия рассчитывается по формуле =((СТЕПЕНЬ(D11-D10;2))*5+(СТЕПЕНЬ(D12-D10;2))*5)/10.

Общая дисперсия рассчитывается по формуле =СУММ(D15;D16).

Вычислим дисперсию и среднее квадратичное отклонение альтернативного признака.

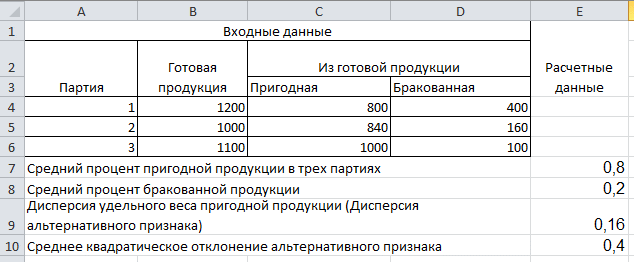
Выпишем формулы, с помощью которых все посчитано:

Средний процент пригодной продукции в трех партиях вычисляется по формуле =(СУММ(C4:C6))/СУММ(B4:B6).

Средний процент бракованной продукции вычисляется по формуле =1-E7

Дисперсия удельного веса пригодной продукции(дисперсия альтернативного признака) вычисляется по формуле =E7*E8.

Среднее квадратичное отклонение рассчитывается по формуле =КОРЕНЬ(E9).

Определение коэффициентов асимметрии и эксцесса предусматривает расчет моментов третьего и четвертого порядка.

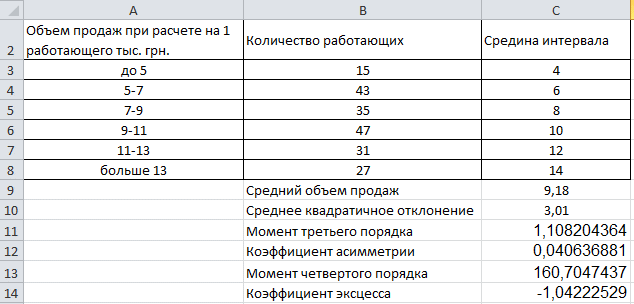
Формулы:

Расчет момента третьего порядка происходит по формуле =(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;3);B3:B8))/СУММ(B3:B8)

Расчет момента четвертого порядка происходит по формуле =(СУММПРОИЗВ(СТЕПЕНЬ(C3:C8-C9;3);B3:B8))/СУММ(B3:B8)

Теперь мы можем рассчитать коэффициент эксцесса по формуле =(C13/СТЕПЕНЬ(C10;4))-3.

С помощью этой работы можно научится анализировать ряды распределения с помощью программы MS Excel.