Ниже дано решение задачи на нахождение дисперсии альтернативного признака. Если же хотите сразу посмотреть нужную формулу - сразу перейдите к формуле дисперсии альтернативного признака.

Задача. За даними інституту досліджень організованого ринку у середньому в 30% форвардних біржових угод порушувались зобов’язання. Визначити дисперсію частки біржових угод, зобов’язання яких порушувались. Відповідь обґрунтуйте.

Задача. По данным института исследований организованного рынка, в среднем в 30% форвардных биржевых соглашений нарушались обязательства. Определить дисперсию части биржевых соглашений, обязательства которых нарушались. Ответ обоснуйте.

Решение.

Поскольку данные представляют собой простой ряд, то для вычисления значения дисперсии нужно применить формулу простой дисперсии.

Формула вычисления простой дисперсии несгруппированного ряда данных

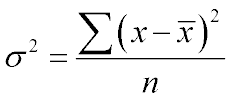
Поскольку размер выборки нам неизвестен, то используем процентные (долевые) вычисления.

Тогда:

Размер выборки будет равен единице (100%) n = 1

Если условия контракта нарушались, то значение конкретного элемента ряда принимаем равным единице.

Тогда, если условия контракта не нарушались, значение элемента принимаем равным нулю.

Откуда среднее значение ряда равно:

( 0,3 х 1 + 0,7 х 0 ) / 1 = 0, 3

Пояснение. 30% значений ряда равно единице, 70% нулю. Разумеется, среднее значение и будет равно 0,3.

Оскільки розмір вибірки нам невідомий, то використовуємо процентні (пайові) обчислення.
Тоді:

Розмір вибірки дорівнюватиме одиниці (100%) n = 1

Якщо умови контракту порушувалися, то значення конкретного елементу ряду набуваємо рівним одиниці.

Тоді, якщо умови контракту не порушувалися, значення елементу набуваємо рівним нулю.
Звідки середнє значення ряду рівне:
( 0,3 х 1 + 0,7 х 0 ) / 1 = 0, 3

Пояснення. 30% значень ряду дорівнює одиниці, 70% нулю. Зрозуміло, середнє значення і буде рівне 0,3.

Теперь нам нужно найти сумму квадратов разностей для всех значений ряда. Поскольку, элементы статистического ряда принимают только значения 0 и 1, то случаев у нас будет два:

( 0 - 0,3 ), если условия контракта не нарушались

( 1 - 0,3 ), если условия контракта нарушались

Зная удельное количество элементов из условия задачи, вычислим дисперсию:

( 0,7 х ( 0 - 0,3 )² + 0,3 x ( 1 - 0,3 )² ) / 1 = 0,21

в более привычном виде:

Тепер нам потрібно знайти суму квадратів різниць для всіх значень ряду. Оскільки, елементи статистичного ряду набувають лише значень 0 і 1, то випадків у нас буде два:

( 0 - 0,3 ), якщо умови контракту не порушувалися
( 1 - 0,3 ), якщо умови контракту порушувалися

Знаючи питому кількість елементів з умови завдання, обчислимо дисперсію:

( 0,7 х ( 0 - 0,3 ) 2 + 0,3 x ( 1 - 0,3 ) 2 ) / 1 = 0,21

в звичнішому вигляді:

Решение задачи на нахождение простой дисперсии несгруппированного ряда

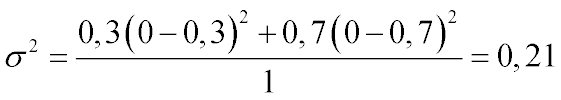Ответ: 0,21

Формула дисперсии альтернативного признака

Исходя из изложенного выше, можно вывести формулу нахождения дисперсии альтернативного признака, если нам известна процентная доля такого признака в общем объеме выборки.

Выведение универсальной формулы для нахождения дисперсии альтернативного признака

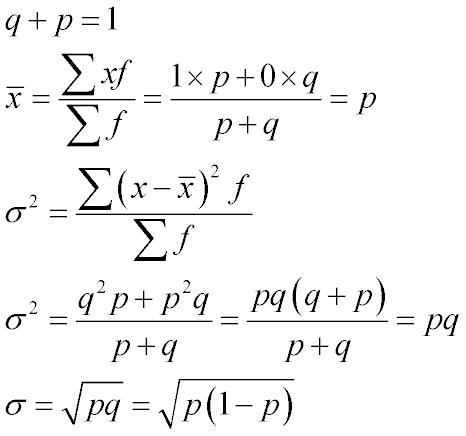
Изначально мы предполагаем, что признак принимает только два значения.

Таким образом, сумма доли элементов, в которых элементы статистического ряда имеют значение признака "нет" и элементов ряда, которые имеют значение признака "да" - равно единице. См. первую формулу.

Для нахождения среднего значения ряда, подставим значения альтернативных признаков ( 0 и 1 ) в формулу нахождения среднего взвешенного значения статистического ряда. Откуда, совершенно очевидно, в знаменателе будет единица, а в числителе - процентное значение элементов "1". То есть ровно процентное значение элементов с признаком "1". (Формула 2)

Формула дисперсии - это средневзвешенное значение квадратов отклонений каждого значения ряда данных. (Формула 3)

Поскольку в нашем ряду данные имеют только два типа значений - "0" и "1", то формула нахождения дисперсии для ряда, имеющего альтернативный признак сводится к Формуле 4.

Пояснение. поскольку мы только что вывели, что среднее значение выборки равно р (Формула 2), то значение квадрата разности значения (0/1) и среднего значения, согласно Формулы 1, будет в первом случае (1-p)² , а во втором случае (1-q)² , теперь, применив следствие из первой формулы: q = 1 - p, p = 1- q . Получим p² и q² . Соответственно, доля значений "0" и "1" равна p и q, в результате в числителе и получается q² p и p² q. Сумма долей признаков значений "0" и "1" согласно Формуле 1 равна 1. В итоге Формула 4 и принимает значение pq, которое и будет равно значению дисперсии альтернативного признака.

Исходя из найденного значения величины дисперсии альтернативного признака, найдем среднеквадратичное отклонение (Формула 5). Поставив значение из Формулы 1 в Формулу 5, получим формулу среднеквадратичного отклонения для дисперсии ряда с альтернативным признаком.

Статистическое распределение выборки | Описание курса | Межгрупповая дисперсия