|
|
Дробь. Дрiб
|
Дроби или отношения, содержащие неизвестные (букву или буквенные выражения) в числителе или знаменателе, нельзя записать целым выражением, не подставив значения неизвестного (буквы). Если буквы делимого или делителя (числителя или знаменателя) представляют собой общий множитель, то тогда, сократив на этот множитель (если он не равен 0), можно дробное рациональное числовое выражение перевести в целое выражение или числовое выражение или упростить.
Для числителя дроби допустимым являются все значения переменных, а для знаменателя – только те, которые не обращают знаменатель в нуль.
Частный случай рациональной дроби – это арифметическая или обыкновенная дробь.
|
Дріб або відносини, що містять невідомі (букву або літерні вирази) у чисельнику або знаменнику, не можна записати цілим виразом, не підставивши значення невідомого (букви). Якщо букви діленого або дільника (чисельника або знаменника) представляють собою загальний множник, то тоді, скоротивши на цей множник (якщо він не дорівнює 0), можна дробове раціональне числове вираження перевести в цілий вираз або числове вираження або спростити.
Для чисельника дробу допустимими є всі значення змінних, а для знаменника - лише ті, які не звертають знаменник в нуль.
Окремий випадок раціонального дробу - це арифметичний або звичайний дріб.
|
Обыкновенная дробь. Звичайний дріб
|
Обыкновенная дробь – это частное двух чисел, записанное определенным образом.
Частное записывается как делимое (верхняя часть дроби) и делитель (нижняя часть дроби), но вместо знака деления («:») между ними ставят горизонтальную черту, которая называется дробной чертой. Делимое называется числителем дроби, а делитель – знаменателем дроби.
Всякая дробь – это отдельная часть целого. Обычно за целое принимается 1 (единица). Число, которое пишут в знаменателе, означает, на сколько равных частей делится целое. Число, которое пишут в числителе, означает сколько объединено этих мелких частей.
Например: дана дробь ¾.
За единое целое (за единицу) условно примем прямоугольник.
|
Звичайний дріб - це частка двох чисел, записане певним чином.
Частка записується як ділене (верхня частина дробу) і дільник (нижня частина дробу), але замість знака ділення («:») між ними ставлять горизонтальну лінію, яка називається дробовою рискою. Ділене називається чисельником дробу, а дільник - знаменником дробу.
Всякий дріб - це окрема частина цілого. Зазвичай за ціле приймається за 1 (одиниця). Число, яке пишуть в знаменнику означає, на скільки рівних частин поділяється ціле. Число, яке пишуть в чисельнику, означає скільки об'єднано цих дрібних частин.
Наприклад: даний дріб ¾.
За єдине ціле (за одиницю) умовно беремо прямокутник.
|

| Знаменатель 4 показывает, что целое (прямоугольник) разделен на 4 равные части: | Знаменник 4 означає, що ціле (прямокутник) розділений на 4 рівні частини: |
| Числитель дроби 3 показывает, что «взято» только 3 части: | Чисельник дробу 3 означає, що «взято» тільки 3 частини: |
| По рисунку видно, что данная дробь по сравнению с целой единицей – меньше. | По малюнку видно, що даний дріб в порівнянні з цілою одиницею – менше. |
|
Значит, дробь ¾ - меньше единицы на ¼. И чтобы получить единицу надо соединить ¾ и ¼.
|
Це означає, що дріб ¾ - менше одиниці на ¼. І щоб отримати одиницю необхідно з’єднати ¾ и ¼.
|
Алгебраическая дробь. Алгебраїчний дрiб
|
Значением алгебраической дроби есть ее преобразование в число (числовое выражение). Чтобы преобразовать дробь, используются законы сложения и умножения, основное свойство дроби, формулы сокращенного умножения.
При решении данной дроби следует оговаривать, что значения неизвестных (числового или буквенного выражения) в знаменателе не равны нулю. Если знаменатель равен нулю или обращается после выполнения всех действий в нуль, то дробь не имеет смысла. Так как сокращать числитель и знаменатель дроби можно только на множители (на слагаемое сокращать дробь нельзя!), то преобразование дробей сводится к выделению, если это возможно, общего множителя в числителе и знаменателе дроби.
|
Значенням алгебраїчного дробу є його перетворення в число (числове вираження). Щоб перетворити дріб, використовуються закони додавання і множення, основна властивість дробу, формули скороченого множення.
При вирішенні даного дробу слід оговорювати, що значення невідомих (числового або літерного виразу) в знаменнику не рівні нулю. Якщо знаменник дорівнює нулю або звертається після виконання всіх дій в нуль, то дріб не має сенсу. Оскільки скорочувати чисельник і знаменник дробу можна тільки на множники (на доданок скорочувати дріб не можна!), то перетворення дробу зводиться до виділення, якщо це можливо, загального множника в чисельнику і знаменнику дробу.
|
|

|
|
Выполняя преобразования (сокращая дробь), мы каждый раз получаем новую дробь или целое выражение, тождественно равные заданной дроби.
ОСНОВНОЕ СВОЙСТВО ДРОБИ
Если числитель и знаменатель дроби умножить или разделить на одно и то же число или выражение, не равное 0, то получим целое число (выражение) или дробь, тождественно равные заданной дроби.
Например:
Числитель и знаменатель дроби – многочлены:
|
Виконуючи перетворення (скорочуючи дріб), ми щоразу отримуємо новий дріб або ціле вираз, тотожне рівні заданої дробу.
ОСНОВНА ВЛАСТИВІСТЬ ДРОБУ
Якщо чисельник і знаменник дробу помножити або розділити на одне і те ж число або вираз, не рівне 0, то отримаємо ціле число (вираз) або дріб, тотожно рівні заданому дробу.
Наприклад:
Чисельник і знаменник дробу - багаточлени:
|
|
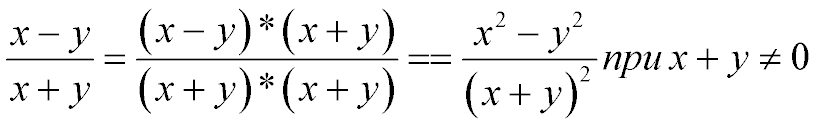
|
|
Используя основное свойство дроби в преобразовании дробей, мы умножили числитель и знаменатель дроби на выражение (многочлен (x+y)) и в числителе и знаменателе получили произведения двучленов.
По формулам сокращенного умножения преобразовали в тождественную заданной дробь (разность квадратов в числителе и квадрат суммы в знаменателе).
Дробь имеет смысл при всех значениях, кроме x=-y
|
Використовуючи основну властивість дробу в перетворенні дробів, ми помножили чисельник і знаменник дробу на вираз (многочлен (x + y)) і в чисельнику і знаменнику здобули множення двочленів.
За формулами скороченого множення перетворили в тотожний заданому дробу (різниця квадратів у чисельнику і квадрат суми в знаменнику).
Дріб має сенс при всіх значеннях, крім x =-y
|
|
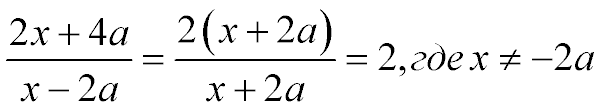
|
|
Для преобразования заданной алгебраической дроби в числителе двучлен заменили на произведение одночлена и двучлена (вынесли за скобки 2) и сократили дробь на общий множитель (x+2a). По основному свойству дроби, сократив числитель и знаменатель на общий множитель, получили целое число, тождественное заданной дроби.
Сократить дробь – это значит разделить числитель и знаменатель дроби на одно и то же число или выражение, исключив значения переменных, которые обращают знаменатель заданной дроби в нуль.
Дроби можно складывать и вычитать, умножать и делить.
|
Для перетворення заданого алгебраїчного дробу у чисельнику двочлен замінили на множення одночлену і двочлену (винесли за дужки 2) і скоротили дріб на загальний множник (x +2a). За основною властивістю дробу, скоротивши чисельник і знаменник на загальний множник, отримали ціле число, тотожне заданому дробу.
Скоротити дріб - це означає розділити чисельник і знаменник дробу на одне і те ж число або вираз, виключивши значення змінних, які звертають знаменник заданого дробу в нуль.
Дріб можна складати і віднімати, множити і ділити.
|
Умножение и деление в столбик |
Описание курса
| Найти наименьшее общее кратное (НОК)
|

