|
|
Свойства арифметического квадратного корня. Властивості арифметичного квадратного кореня
| 1. Квадратный корень из произведения двух неотрицательных множителей равен произведению корней из этих множителей: | 1. Квадратний корінь з добутку двох невід'ємних множників дорівнює добутку коренів з цих множників: |
a≥0, b≥0
| 2. Квадратный корень из дроби, числитель которой неотрицательный, а знаменатель положительный, равен корню из числителя, разделенному на корень из знаменателя: | 2. Квадратний корінь з дробу, чисельник якої ненегативний, а знаменник - позитивний, дорівнює кореню з чисельника, розділеному на корінь із знаменника: |
a≥0, b>0
Преобразование арифметических квадратных корней. Перетворення арифметичних квадратних коренів
|
Чтобы извлечь квадратный корень из многочлена, надо вычислить многочлен и из полученного числа извлечь корень.
Внимание! Нельзя извлекать корень из каждого слагаемого (уменьшаемого и вычитаемого) отдельно.
Например:
|
Щоб витягти квадратний корінь з многочлена, треба обчислити багаточлен і з отриманого числа витягти корінь.
Увага! Не можна витягати корінь з кожного додатку (зменшуваного і від’ємного) окремо.
Наприклад:
|
|
Чтобы извлечь квадратный корень из произведения (частного), можно вычислить корень квадратный из каждого множителя (делимого и делителя), а полученные значения взять произведением (частным).
Например:
|
Щоб витягти квадратний корінь з добутку (частки), можна обчислити корінь квадратний з кожного множника (діленого і дільника), а отримані значення взяти добутком (часткою).
Наприклад:
|
|
Чтобы извлечь квадратный корень из дроби, надо извлечь квадратный корень из числителя и знаменателя отдельно, а полученные значения оставить дробью или вычислить как частное (если возможно это по условию).
Например:
|
Щоб витягти квадратний корінь з дробу, треба витягти квадратний корінь з чисельника і знаменника окремо, а отримані значення залишити дробом або обчислити як частку (якщо можливо це за умовою).
Наприклад:
|
|
Из-под знака корня можно вынести множитель и можно внести множитель под знак корня. При вынесении множителя из него извлекается корень, а при внесении - он возводится в соответствующую степень.
Например:
|
З-під знака кореня можна винести множник і можна внести множник під знак кореня. При винесенні множника з нього витягується корінь, а при внесенні - він зводиться у відповідну ступінь.
Наприклад:
|
| Если корень в знаменателе дроби, то такую дробь можно заменить тождественной ей дробью, не содержащей радикалов (корней) в знаменателе. Для этого умножают числитель и знаменатель дроби на такое выражение (сопряженное знаменателю), чтобы корень в знаменателе извлекался. | Якщо корінь в знаменнику дробу, то такий дріб можна замінити тотожним йому дробом, що не містить радикалів (коренів) у знаменнику. Для цього множать чисельник і знаменник дробу на такий вираз (поєднане зі знаменником), щоб корінь в знаменнику видалявся. |
Примеры. Приклади
| 1. Избавиться от радикала в знаменателе дроби: | 1. Позбутися від радикала в знаменнику дробу: |
| 2. Избавиться от радикала в знаменателе дроби: | 2. Позбутися від радикала в знаменнику дробу: |
| 3. Избавиться от радикала в числителе дроби: | 3. Позбутися від радикала в чисельнику дробу: |
| Освобождение дроби от радикалов в числителе (в знаменателе) дроби называется преобразованием алгебраической дроби.
| Звільнення дробу від радикалів у чисельнику (в знаменнику) дробу називається перетворенням алгебраїчного дробу.
|
|
Чтобы преобразовать сумму (разность) квадратных корней, нужно привести подкоренные выражения к одному основанию степени, если это возможно, извлечь корни из степеней и записать их перед знаками корней, а оставшиеся квадратные корни с одинаковыми подкоренными выражениями можно сложить, для чего складываются коэффициенты перед знаком корня и дописывается тот же квадратный корень.
Пример 4:
|
Щоб перетворити суму (різницю) квадратних коренів, потрібно привести підкоренні вирази до однієї основи ступеня, якщо це можливо, отримати коріння ступенів і записати їх перед знаками коренів, а решта квадратні корені з однаковими підкореними виразами можна скласти, для чого складаються коефіцієнти перед знаком кореня і дописується той же квадратний корінь.
Приклад 4:
|
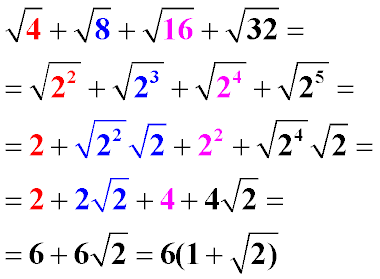
|
Приведем все подкоренные выражения к основанию 2.
Из четной степени корень извлекается полностью, из нечетной степени корень основания в степени 1 оставляем под знаком корня.
Приводим подобные целые числа и коэффициенты складываем с одинаковыми корнями. Запишем двучлен как произведение числа и двучлена суммы.
Пример 5:
|
Наведемо всі підкорені вирази до основи 2.
З парного ступеня корінь витягується повністю, з непарного ступеня корінь основи в ступені 1 залишаємо під знаком кореня.
Наводимо подібні цілі числа і коефіцієнти складаємо з однаковим корінням. Запишемо двочлен як добуток числа і двочлена суми.
Приклад 5:
|
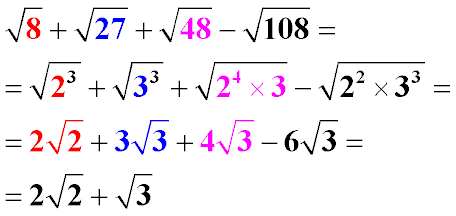
|
Приводим подкоренные выражения к наименьшему основанию или произведению степеней с наименьшими основаниями. Из четных степеней подкоренных выражений извлекаем корень, остатки в виде основания степени с показателем 1 или произведением таких оснований оставляем под знаком корня. Приводим подобные члены (складываем коэффициенты одинаковых корней).
Пример 6:
|
Наводимо підкорені вирази до найменшої основи або добутку ступенів з найменшими основами. З парних ступенів підкорених виразів витягаємо корінь, залишки у вигляді основи ступеня з показником 1 або добутком таких основ залишаємо під знаком кореня. Наводимо подібні члени (складаємо коефіцієнти однакових коренів).
Приклад 6:
|
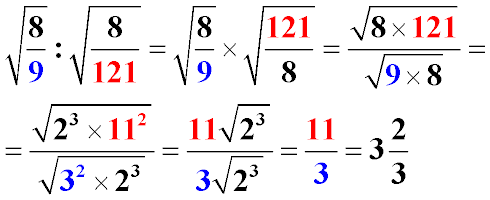
|
Заменим деление дробей на умножение (с заменой второй дроби на обратную). Перемножим отдельно числители и знаменатели дробей. Под каждым знаком корня выделим степени. Сократим одинаковые множители в числителе и знаменателе. Извлечем корни из четных степеней.
Пример 7:
|
Замінимо ділення дробів на множення (з заміною другого дробу на зворотний). Перемножимо окремо чисельники і знаменники дробів. Під кожним знаком кореня виділимо ступені. Скоротимо однакові множники в чисельнику і знаменнику. Винесемо коріння з парних ступенів.
Приклад 7:
|
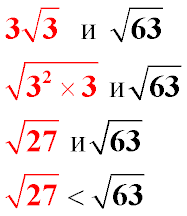
|
Чтобы сравнить два квадратных корня, их подкоренные выражения надо привести в степени с одинаковым основанием, тогда чем больше показать степени подкоренного выражения, тем больше значение квадратного корня.
В этом примере привести к одному основанию подкоренные выражения нельзя, так как в первом основание 3, а во втором – 3 и 7.
Второй способ сравнения состоит в том, чтобы внести коэффициент корня в подкоренное выражение и сравнить числовые значения подкоренных выражений. У квадратного корня чем больше подкоренное выражение, тем больше значение корня.
Пример 8:
|
Щоб порівняти два квадратних кореня, їх підкорені вирази треба привести до ступеня з однаковою основою, тоді чим більше показник степеня підкореневого виразу, тим більше значення квадратного кореня.
У цьому прикладі привести до одної основи підкорені вирази не можна, так як в першому основа 3, а у другому - 3 і 7.
Другий спосіб порівняння полягає в тому, щоб внести коефіцієнт кореня в підкореневий вираз і порівняти числові значення підкорених виразів. У квадратного кореня чим більше підкореневий вираз, тим більше значення кореня.
Приклад 8:
|
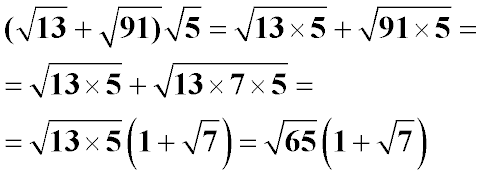
|
Используя распределительный закон умножения и правило умножения корней с одинаковыми показателями (в нашем случае – квадратных корней), получили сумму двух квадратных корней с произведением под знаком корня. Разложим 91 на простые множители и выносим корень за скобки с общими подкоренными множителями (13*5).
Мы получили произведение корня и двучлена, у которого один из одночленов целое число (1).
Пример 9:
|
Використовуючи розподільний закон множення і правило множення коренів з однаковими показниками (в нашому випадку - квадратних коренів), отримали суму двох квадратних коренів з добутком під знаком кореня. Розкладемо 91 на прості множники і виносимо корінь за дужки із загальними підкореневими множниками (13*5).
Ми отримали добуток кореня і двочлена, у якого один з одночленів ціле число (1).
Приклад 9: |
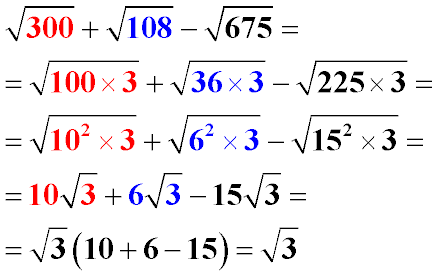
|
В подкоренных выражениях выделим множителями числа, из которых можно извлечь целый квадратный корень. Извлечем квадратные корни из степеней и поставим числа коэффициентами квадратных корней.
У членов данного многочлена есть общий множитель √3, который можно вынести за скобки. Приведем подобные слагаемые.
Пример 10:
|
У підкореневих виразах виділимо множниками числа, з яких можна отримати цілий квадратний корінь. Винесемо квадратні корені із ступенів і поставимо числа коефіцієнтами квадратних коренів.
У членів даного многочлена є спільний множник √3, який можна винести за дужки. Наводимо подібні доданки.
Приклад 10:
|
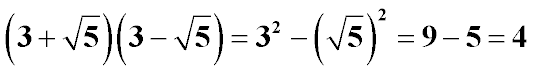
|
Произведение суммы и разности двух одинаковых оснований (3 и √5) по формуле сокращенного умножения можно записать как разность квадратов оснований.
Корень квадратный в квадрате всегда равен подкоренному выражению, поэтому мы избавимся от радикала (знака корня) в выражении.
|
Добуток суми і різниці двох однакових основ (3 і √5) з формули скороченого множення можна записати як різницю квадратів основ.
Корінь квадратний у квадраті завжди дорівнює підкореневому виразу, тому ми позбудемося радикала (знака кореня) у виразі.
|
Квадратный корень. Квадратний корінь |
Описание курса
| Таблица степеней натуральных чисел
|

