Показательная функция. Показова функція

Определение показательной функции. Визначення показової функції

По определению показательной функции у=а^х, а>0 и а≠1; а=const – основание; х – переменная (аргумент).

Показательная функция возрастает для всех xϵR, если a>1, и убывает, если 0<a<1.

З визначення показової функції у=а^х, а>0 і а≠1; а=const - основа; х - змінна (аргумент).

Показова функція зростає для всіх xϵR, якщо a>1 і спадає, якщо 0<a<1.

График экспоненциальной функции и ее пересечения с осями. Графік експоненціальної функції і її пересічення з осями.

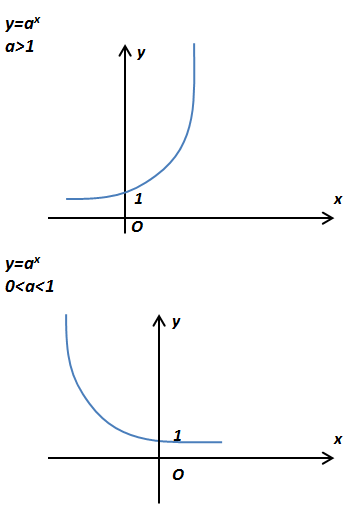
Область значений: yϵ(0;∞). (Все значения у положительны – т.е. график показательной функции всегда расположен выше оси Оx).

Если основанием является е=2,7182818284590…, то касательная, проведенная к кривой у=е^х в точке ее пересечения с осью Оу (х=0), образует с осью Ох угол 45°. Кривая у=а^х (или у=е^х) называется экспонентой.

Основание натурального логарифма:

Область значень: yϵ(0;∞). (Все значення у позитивні - тобто графік показової функції завжди розташований вище осі Ох).

Якщо підставою є е=2,7182818284590..., то дотична, проведена до кривої у=е^х в точці її перетину з віссю Оу (х=0), утворює з віссю Ох кут 45°. Крива у=а^х(або у=е^х) називається експонентою.

Основа натурального логарифму:

Определение значения числа e. Визначення значення числа e.

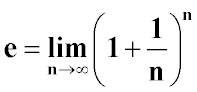
Пример 1. Необходимо решить уравнение, в котором неизвестное является степенью простой дроби, представленной в виде квадратного уравнения.
У нас есть простая дробь ( 1/5 ), степень которой - квадратное уравнение. Для решения этого примера нам необходимо преобразовать основание степени таким образом, чтобы свести выражение к равным основаниям. Из равенства оснований будет следовать равенство показателей.
Числитель и знаменатель правой части умножим на √5 (Итерация 2).
Произведение двух √5 даст нам пять, что позволит сократить числитель и знаменатель (Итерация 3).
Поскольку извлечение квадратного корня тождественно возведению в степень 1/2, а единица в любой степени все равно даст единицу, получаем итерацию 4.
Из равенства оснований (1/5) следует равенство показателей (Итерация 5). Как видно, степенью дроби является квадратное уравнение. Это позволяет свести решение к решению квадратного уравнения.

Приклад 1. Необхідно вирішити рівняння, в якому невідоме є мірою простого дробу, представленого у вигляді квадратного рівняння.
У нас є простий дріб ( 1/5 ), міра якого - квадратне рівняння. Для вирішення цього прикладу нам необхідно перетворити підставу міри так, щоб звести вираження до рівних підстав. З рівності підстав виходитиме рівність показників.
Чисельник і знаменник правої частини помножимо на √5 (Ітерація 2).
Твір двох √5 дасть нам п'ять, що дозволить скоротити чисельник і знаменник (Ітерація 3).
Оскільки витягання квадратного кореня тотожне обчисленню ступеня 1/2, а одиниця в будь-якій мірі все одно дасть одиницю, отримуємо ітерацію 4.
З рівності підстав (1/5) виходить рівність показників (Ітерація 5). Як видно, мірою дробу є квадратне рівняння. Це дозволяє звести рішення до вирішення квадратного рівняння.

Решение примера, в котором дробь имеет степень, являющуюся квадратным уравнением. Вирішення прикладу, в якому дріб має міру, що є квадратним рівнянням.

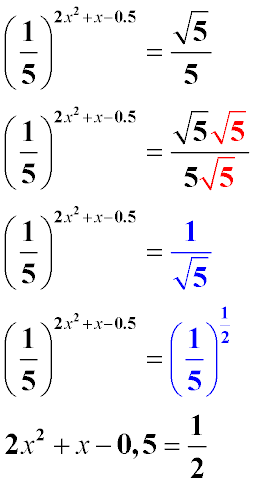
2x²+x-1=0

x₁=-1; x₂=1/2.

Уравнения a^f⁽^x)=b^ϕ⁽^x), a>0, b>0 решаются сведением обеих их частей к общему основанию, а затем из равенства степеней с одинаковым основанием следует равенство показателей.

Пример 2. Решить неравенство, в котором неизвестное (икс) является степенью (показателем) дроби

2x²+x-1=0

x₁=-1; x₂=1/2.

Рівняння a^f⁽^x)=b^ϕ⁽^x), a>0, b>0 вирішуються зведенням обох їх частин спільної основи, а потім рівності ступенів з однаковим підставою слід рівність показників.

Приклад 2. Вирішити нерівність, в якій невідоме (ікс) є мірою (показником) дробу

Решение неравенства, в котором неизвестное является степень дроби. Вирішення нерівності, в якій невідоме є міра дробу.

Преобразуем 1,5 в простую дробь, а корень представим в виде степени (Итерация 2)
Поскольку возведение степень минус единица эквивалентно получению дроби, обратной данной, получим Итерацию 3
Так как основанием степени является правильная простая дробь, то рост переменной, являющейся показателем степени, будет эту дробь уменьшать, примем во внимание, что знак неравенства необходимо поменять на противоположный. Получаем ответ (Итерация 4).

Перетворемо 1,5 в простий дріб, а корінь представимо у вигляді міри (Ітерація 2)
Оскільки міра в значеннi мінус одиниця еквівалентна здобуттю дробу, зворотного даному, отримаємо Ітерацію 3
Оскільки основою міри є правильний простий дріб, то зростання змінної, що є показником, цей дріб зменшуватиме, візьмемо до уваги, що знак нерівності необхідно поміняти на протилежний. Отримуємо відповідь (Ітерація 4).

Таблица степеней натуральных чисел | Описание курса | Функции