См. также:

Производная корня. Формулы для нахождения производной корня

Формула нахождения производной квадратного корня, кубического корня и корня произвольной степени

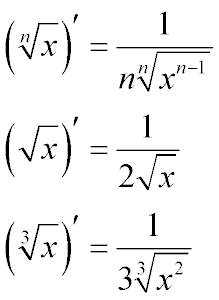
Общий случай формулы производной корня произвольной степени - дробь,
в числителе которой единица, а в знаменателе число, равное степени корня, для которого вычислялась
производная, умноженная на корень такой же степени, подкоренное выражение которого - переменная
в степени корня, для которого вычислялась производная, уменьшенной на единицу
Производная квадратного корня - является частным случаем предыдущей формулы.
Производная квадратного корня из x - это дробь, числитель которого равен единице,
а знаменатель - двойка, умноженная на квадратный корень х
Производная кубического корня, также частный случай общей формулы.
Производная кубического корня - это единица, деленная на три кубических корня из икс квадрат.

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного
и кубического корня именно такие, как приведены на рисунке.

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение
корня производной степени - это то же самое, что возведение в степень дроби, знаменатель которой
равен той же степени. Тогда нахождение производной корня сводится к применению формулы
нахождения производной степени соответствующей дроби.

Производная переменной под квадратным корнем

( √x )' = 1 / ( 2√x ) или 1/2 х^-1/2

Пояснение:
( √x )' = ( х^1/2 )'

Квадратный корень - это точно то же самое действие, что и возведение в степень 1/2,
значит для нахождения производной корня можно применить формулу из правила нахождения производной
от переменной в произвольной степени:

( х^1/2 )' = 1/2 х^-1/2 = 1 / (2√х)

Производная кубического корня (производная корня третьей степени)

Производная кубического корня находится точно по такому же принципу, что и квадратного.

Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования.
Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.

Нахождение производной кубического корня представлением через степенную функцию

Степень -2/3 получается в следствие вычитания единицы из 1/3

Производная переменной под корнем произвольной степени

Данная формула пригодна для нахождения производной корня любой степени:

( ⁿ√x )' = 1 / ( n ⁿ√x^n-1 )

В более удобном для глаза виде она представлена на картинке выше.

Здесь:

n - степень корня, для которой находится производная

x - переменная, для которой находится производная

2080.1947

Производная дроби | Описание курса | Производная логарифма