|
|
Свойства бесконечно малых и бесконечно больших функций
В дальнейшем для краткости будем называть функции бесконечно малые и бесконечно большие.
- Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малой функцией.
- Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция в данной точке.
- Произведение бесконечно малых функций есть бесконечно малая функция.
- Сумма бесконечно больших функций одного знака есть бесконечно большая функция.
- Произведение бесконечно больших функций есть бесконечно большая функция.
- Частное двух бесконечно малых функций f1 / f2 является неопределенностью вида «0/0».
- Разность двух бесконечно больших функций одного знака есть неопределенность вида «∞-∞».
-
Если f(x) при x→x0 есть бесконечно малая функция, то 1 / f(x) в том же предельном переходе есть бесконечно большая функция.
Второе определение предела функции при x→x0
Если при x→x0 предел функции f(x) равен A, то разность f(x)−A=α, где α – бесконечно малая функция.
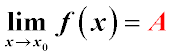
Обратное утверждение: если при x→x0 функцию f(x) можно представить в виде суммы некоторого числа A и бесконечно малой функции,
т.е. f(x)=A+α, то предел функции f(x) при x→x0 равен A.
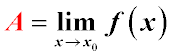
Дополнительные свойства и примеры
-
Свойства бесконечно малых функций:
-
Если f(x) и g(x) – бесконечно малые функции при x→x0, то их сумма f(x)+g(x) также является бесконечно малой функцией.
-
Если f(x) – бесконечно малая функция при x→x0, а g(x) – ограниченная функция, то произведение f(x)⋅g(x) является
бесконечно малой функцией.
-
Свойства бесконечно больших функций:
-
Если f(x) и g(x) – бесконечно большие функции при x→x0, то их сумма f(x)+g(x) также является бесконечно большой функцией.
-
Если f(x) – бесконечно большая функция при x→x0, то 1/f(x) является бесконечно малой функцией.
-
Примеры:
-
Пусть f(x)=1/x при x→0. Тогда f(x) является бесконечно большой функцией, а 1 / f(x) = x является бесконечно малой функцией.
-
Пусть f(x)=x2 и g(x)=x3 при x→0. Тогда f(x) и g(x) являются бесконечно малыми функциями, и их сумма f(x)+g(x)=x2+x3
также является бесконечно малой функцией.
Эллипс |
Описание курса
| Уравнения
|

