|
|
См. также: более простой уровень - сложение и вычитание простых дробей для младших классов.
Сложение и вычитание дробей. Додавання і віднімання дробів
|
Сложение (вычитание) дробей производится по правилам сложения (вычитания) обыкновенных дробей.
Слагаемыми, уменьшаемым и вычитаемым в числителе или знаменателе дроби могут быть любые рациональные числа или выражения с переменными. Исключения составляют число 0 и выражения, обращающие знаменатель в нуль.
Правило: Чтобы сложить (вычесть) дроби с одинаковым знаменателем, не равным нулю, нужно сложить (вычесть) их числители и оставить тот же знаменатель.
Чтобы сложить (вычесть) дроби с разными знаменателями, не равными нулю, нужно найти общий знаменатель дробей и дополнительные множители. Умножить числители на дополнительные множители и взять произведения слагаемыми (от первого произведения вычесть второе), оставить общий знаменатель под суммой (разностью).
Рассмотрим сложение и вычитание дробей на примерах:
|
Додавання (віднімання) дробів проводиться за правилами складання (віднімання) звичайних дробів.
Доданками, зменшуваним і від'ємником в чисельнику або знаменнику дробу можуть бути будь-які раціональні числа або вирази зі змінними. Винятки становлять число 0 і вирази, які звертають знаменник в нуль.
Правило: Щоб додати (відняти) дроби з однаковим знаменником, не рівним нулю, треба додати (відняти) їх чисельники і знаменник залишити той самий.
Щоб додати (відняти) дроби з різними знаменниками, не рівними нулю, потрібно знайти спільний знаменник дробів і додаткові множники. Помножити чисельники на додаткові множники і взяти добуток складовими (від першого добутку відняти другий), залишити спільний знаменник під сумою (різницею).
Розглянемо додавання і віднімання дробів на прикладах:
|
Примеры сложения и вычитания простых дробей. Приклади складання та віднімання звичайних дробів
| ЗАДАЧА 1: Сумма дробей, у которых знаменатели одинаковые (произведение одночлена на многочлен), а числители: у первой дроби – многочлен, у второй дроби – одночлен. | ЗАВДАННЯ 1: Сума дробів, у яких однакові знаменники (добуток одночлена на багаточлен), а чисельники: у першому дробу - багаточлен, у другому - одночлени. |
|

Так как знаменатели дробей одинаковые, то сложим числители дробей и подпишем тот же знаменатель.
В числителе выражение x2+y2+2xy можно заменить по формулам сокращенного умножения на квадрат двучлена, так как, используя переместительный закон сложения, трехчлен можно записать как x2+2xy+y2.
|

Так як знаменники дробів однакові, то складемо чисельники дробів і підпишемо той же знаменник.
В чисельнику виразу x2+y2+2xy можна замінити за формулами скороченого множення на квадрат двочлена, так як, використовуючи переміщуючий закон додавання, тричлен можна записати як x2+2xy+y2.
|
|
при а≠0, х≠-у.
Квадрат любого основания есть произведение двух одинаковых сомножителей, поэтому в числителе вместо квадрата суммы пишем произведение одинаковых двучленов, один из которых можно сократить с таким же двучленом в знаменателе.
Сумма имеет смысл при любых а, кроме а=0, х=-у.
|
при а≠0, х≠-у.
Квадрат будь-якої основи є добуток двох однакових співмножників, тому в чисельнику замість квадрата суми пишемо добуток однакових двочленів, один з яких можна скоротити з таким же двочленом в знаменнику.
Сума має сенс при будь-яких а, крім а=0, х=-у.
|
| ЗАДАЧА 2: Разность двух алгебраических дробей с одинаковыми знаменателями. Числители и знаменатели обеих дробей – многочлены. | ЗАДАЧА 2: Різниця двох алгебраїчних дробів з однаковими знаменниками. Чисельники і знаменники обох дробів - багаточлени. |
| В числителе полученной дроби приведем подобные, а в знаменателе трехчлен заменим по формуле сокращенного умножения на квадрат разности, который можно записать как произведение двух одинаковых множителей: | У чисельнику отриманого дробу наведемо подібні, а в знаменнику тричлен змінимо за формулою скороченого множення на квадрат різниці, який можна записати як добуток двох однакових множників: |
|
при a-b≠0.
Числитель и знаменатель имеют одинаковый множитель-двучлен, на который их можно по основному свойству дроби сократить. Решение будет верным при всех значениях а и в, кроме а=в.
|
при a-b≠0.
Чисельник і знаменник мають однаковий множник-двочлен, на який їх можна за основною властивістю дробу скоротити. Рішення буде вірним при всіх значеннях а ів, крім а=в.
|
| ЗАДАЧА 3: Сумма двух дробей с одинаковыми знаменателями, которые представлены одночленами в числителях и многочленом – в знаменателях. | ЗАДАЧА 3: Сума двох дробів з однаковими знаменниками, які представлені одночленами в чисельниках і багаточленом - в знаменниках. |
|
В числителе сумма кубов заменяем по формуле сокращенного умножения на произведение двучлена и трехчлена.
Сократим общий двучлен числителя и знаменателя по основному свойству дроби.
Результатом является целое выражение:
|
У чисельнику суму кубів замінюємо за формулою скороченого множення на добуток двочлена і тричлена.
Скоротимо загальний двочлен чисельника та знаменника за основною властивістю дробу.
Результатом є цілий вираз:
|
| ЗАДАЧА 4:Разность дробей с разными знаменателями, у которых числители и знаменатели – одночлены. | ЗАДАЧА 4:Різницю дробів з різними знаменниками, у яких чисельники і знаменники - одночлени. |
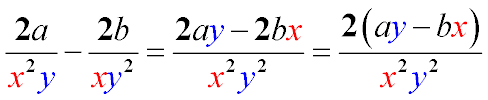
|
при х≠0, у≠0.
Найдем общий знаменатель дробей как произведение оснований с наибольшими показателями степеней. Проставим дополнительные множители.
Умножим одночлены числителей на их дополнительные множители и запишем произведения разностью одночленов, а в знаменателе – общий знаменатель.
Из числителя выносим общий множитель (2) и записываем числитель как произведение одночлена на многочлен.
Дальнейшее преобразование невозможны, дробь имеет решения при всех значениях переменных, кроме х=у=0.
|
при х≠0, у≠0.
Знайдемо загальний знаменник дробів як добуток основ з найбільшими показниками ступенів. Проставимо додаткові множники.
Помножимо одночлени чисельників на їх додаткові множники і запишемо добутки різницею одночленів, а в знаменнику - загальний знаменник.
З чисельника виносимо загальний множник (2) і записуємо чисельник як добуток одночлена на багаточлен.
Подальші перетворення неможливі, дріб має рішення при всіх значеннях змінних, крім х=у=0.
|
| ЗАДАЧА 5: Сумма дробей с разными знаменателями, у которых числители и знаменатели – многочлены. | ЗАДАЧА 5: Сума дробів з різними знаменниками, у яких чисельники і знаменники - багаточлени. |
|
Общий знаменатель дробей равен произведению их знаменателей. Проставим дополнительные множители, умножим числители на их дополнительные множители и произведения возьмем суммой. Подпишем под числителем общий знаменатель.
Перемножим в числителях многочлены и запишем одним многочленом. В знаменателе произведение двучленов по формуле сокращенного умножения переведем в многочлен (разность квадратов):
|
Спільний знаменник дробів дорівнює добутку їх знаменників. Проставимо додаткові множники, помножимо чисельники на їх додаткові множники і добутки візьмемо сумою. Підпишемо під чисельником спільний знаменник.
Перемножимо в чисельниках багаточлени і запишемо одним багаточленом. У знаменнику твір двочленів за формулою скороченого множення переведемо в багаточлен (різниця квадратів):
|
| Приведем подобные слагаемые в числителе: | Наведемо подібні доданки в чисельнику: |
|
при х2-у2≠0.
Получилась дробь, у которой в числителе и знаменателе двучлены.
Из числителя можно вынести общий множитель (2), но это не упростит дробь.
Все действительные значения неизвестных будут решением дроби, кроме х=±у, что обращает знаменатель в 0.
|
при х2-у2≠0.
Вийшов дріб, у якому в чисельнику і знаменнику двочлени.
З чисельника можна винести спільний множник (2), але це не спростить дріб.
Всі дійсні значення невідомих будуть рішенням дробу, крім х=±у, що звертає знаменник на 0.
|
Сложение и вычитание простых дробей |
Описание курса
| Вычислить выражение с простыми и десятичными дробями
|

