Задача

Вычислите значение выражения

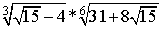
Решение.

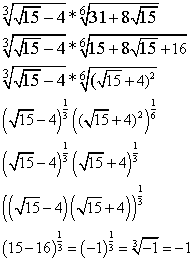
Пояснение.
Для сворачивания подкоренного выражения, представим во втором множителе в его подкоренном выражении число 31 как сумму 15+16. (строка 2)

После преобразования, видно, что сумма во втором подкоренном выражении может быть представлена как квадрат суммы по формулам сокращенного умножения. (строка 3)

Теперь представим каждый корень из данного произведения как степень. (строка 4)

Упростим выражение (строка 5)

Поскольку степень произведения равна произведению степеней каждого из множителей, представим это соответствующим образом (строка 6)

Как видно, по формулам сокращенного умножения имеем разность квадратов двух чисел. Откуда и вычислим значение выражения (строка 7)

Задача

Вычислите значение выражения.

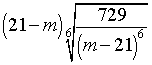
Решение.

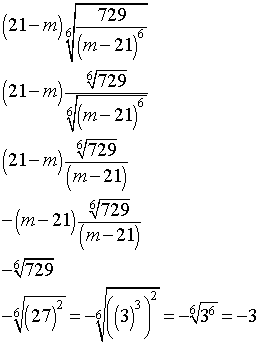
Пояснение.

Используем свойства корня, что корень произвольной степени частного чисел равен частному корней этих чисел (строка 2)

Корень произвольной степени числа этой же степени равен этому числу (строка 3)

Вынесем из скобки первого множителя минус. При этом все знаки внутри скобки поменяются на противоположные (строка 4)

Выполним сокращение дроби (строка 5)

Представим число 729 как квадрат числа 27, а число 27 как куб числа 3. Откуда и получим значение подкоренного выражения.