Геометрический смысл производной

ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К КРИВОЙ

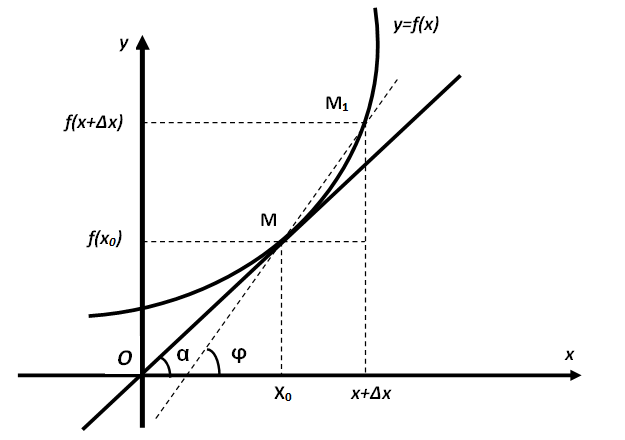
Касательной к кривой y=ƒ(x) в точке М называется предельное положение секущей, проведенной через точку М и соседнюю с ней точку М₁ кривой,
при условии, что точка М₁ неограниченно приближается вдоль кривой к точке М.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Производная функции y=ƒ(x) в точке х₀ численно равна тангенсу угла наклона к оси Ох касательной, проведенной к кривой y=ƒ(x) в точке М (х₀; ƒ(x₀)).

Иными словами, производная показывает, насколько резко изменяется функция в данной точке. Если угол наклона касательной большой, то изменение
происходит быстро, если угол мал – изменение медленное.

Практический смысл производной

Рассмотрим, что означает величина, найденная нами как производная функции.

Прежде всего, производная – это скорость изменения функции в данной точке. Она показывает, как быстро изменяется значение функции
при малом изменении аргумента.

Что такое "скорость изменения"? Представим себе функцию f(x) = 5. Вне зависимости от значения аргумента , ее значение остается постоянным.
То есть, скорость ее изменения равна нулю, а производная будет также равна нулю:

f'(x) = 0

Теперь рассмотрим функцию f(x) = x. Производная равна единице, что означает: если увеличивается на единицу, то значение функции тоже
увеличивается на единицу. Это можно записать так:

Если мы возьмем функцию f(x) = x², ее производная будет f'(x) = 2x. Это означает, что скорость изменения функции зависит от x:
чем больше x, тем быстрее увеличивается f(x).

Вторичная производная и ускорение

Если первая производная показывает скорость изменения функции, то вторая производная показывает, как изменяется эта скорость,
то есть ускорение.

Например, рассмотрим функцию f(x) = x². Мы уже знаем, что ее первая производная равна f'(x) = 2x. Найдем вторую производную:

Это означает, что скорость изменения функции постоянно увеличивается с одинаковой интенсивностью. Если вторая производная положительная,
функция ускоряется (график изгибается вверх), если отрицательная – замедляется (график изгибается вниз).

Интуитивное объяснение на примере движения

Допустим, мы едем на автомобиле.

• Производная скорости – это ускорение: если ускорение положительное, машина разгоняется, если отрицательное – замедляется.

• Если производная постоянна, движение равномерное.

• Если скорость изменяется быстро, производная большая.