|
См. также полную таблицу производных простых функций.
Производная дроби 1/x
Формулы нахождения производной дроби как для частного случая, так и универсальную, можно посмотреть внизу страницы. Далее, же следует подробное описание вывода этих формул с подробным пояснением, почему именно так.
Для начала, преобразуем выражение для нахождения производной. Как известно, дробь вида 1/х можно представить как х-1.
Таким образом, заменив исходное выражение на тождественное, задачу нахождения производной дроби вида 1/х можно представить как:
(1/x)' = (x -1)'
Тогда для нахождения производной дроби можно применить правило нахождения производной степенной функции, откуда:
(x -1)' = -1x-2 = - 1 / х2
Таким образом, производная дроби 1/х равна:
(1/х)' = - 1 / x2
На основании только что показанного принципа преобразования исходного выражения, можно вывести и более универсальную формулу:
Производная дроби с переменной произвольной степени в знаменателе
( 1 / xс )' = - c / xс+1
Пример нахождения производной дроби:
( 1 / x2 )' = - 2 / x3 .
(впереди ставим минус, показатель степени переменной поднимаем в числитель дроби, а степень переменной в знаменателе увеличиваем на единичку. Немного "ненаучно", но подходит для быстрого запоминания)
Формулы нахождения производной дроби:
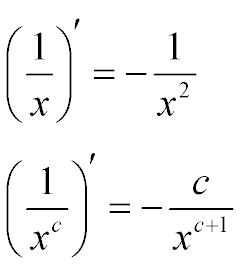
Производная числа |
Описание курса
| Производная корня
|

