|
|
Quadrilateral Definition
A quadrilateral is a polygon with four vertices, three of which do not lie on the same line.
A quadrilateral is a geometric figure consisting of four points, three of which do not lie on one straight line, connected in series by segments.
Properties of quadrilaterals
The quadrilateral can be:
- self-intersecting
-
non-convex
-
convex

A self-intersecting quadrilateral is a quadrilateral in which any of its sides have an intersection point (in blue in the figure).
A non-convex quadrilateral is a quadrilateral in which one of the interior angles is greater than 180 degrees (indicated in red in the figure)
The sum of the angles of any quadrilateral that is not self-intersecting is always 360 degrees.
Special types of quadrilaterals
Quadrangles can have additional properties, forming special types of geometric shapes:
- Parallelogram
-
Rhombus
-
Rectangle
-
Square
-
Trapeze
-
Deltoid
-
Counterparallelogram
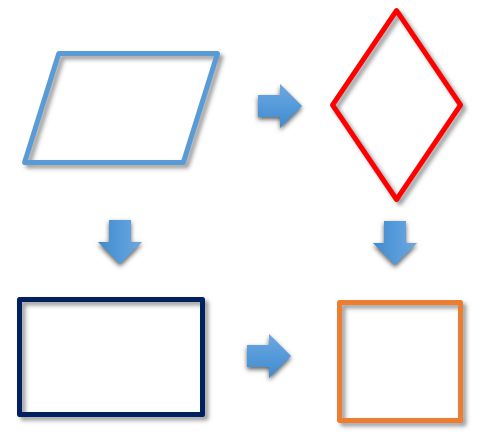
You can learn more about each of the special types of quadrilateral by clicking on the links above.
As can be seen from the figure, special types of quadrilaterals inherit the properties of their "ancestors".
For example, a rectangle (shown in dark blue in the figure) is a special case of a parallelogram (shown in blue in the figure).
Thus, he retains all his properties and adds his own, special ones.
Therefore, when solving problems about rectangles, you can apply all the properties and theorems of a parallelogram.
A square (shown in orange in the figure) is a special case of a rectangle.
That is, a square has all the properties of a parallelogram, a rectangle, as well as its own, special ones.
But, most interestingly, the square is also a special case of a rhombus (shown in red in the figure),
that is, in addition to those indicated (parallelogram, rectangle), it also has all the properties of a rhombus.
Also, interesting special cases of the quadrilateral are the trapezoid and the deltoid.
Quadrilateral and circle (Quadrangular and circle)
A quadrilateral inscribed around a circle (a circle inscribed in a quadrilateral).
The main property of the circumscribed quadrilateral:
A quadrilateral can be circumscribed around a circle if and only if the sums of the lengths of opposite sides are equal.
Quadrilateral inscribed in a circle (circle inscribed around a quadrilateral)
Main property of an inscribed quadrilateral:
A quadrilateral can be inscribed in a circle if and only if the sum of the opposite angles is 180 degrees.
Quadrilateral side length properties
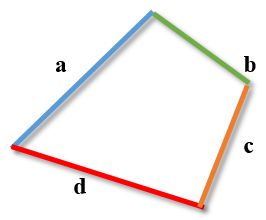
The modulus of the difference of any two sides of a quadrilateral does not exceed the sum of its other two sides.
|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b
Important. The inequality is true for any combination of sides of a quadrilateral. The figure is provided solely for ease of understanding.
In any quadrilateral, the sum of the lengths of its three sides is not less than the length of the fourth side.
a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c
Important. When solving problems within the school curriculum, you can use strict inequality (<).
Equality is achieved only if the quadrilateral is "degenerate", that is, its three points lie on the same straight line.
That is, this situation does not fall under the classical definition of a quadrilateral.
The ratio of sides and diagonals can be expressed by the formula
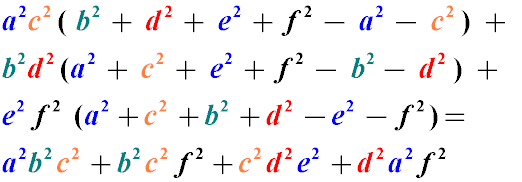
Ptolemy's inequality
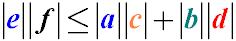
The product of the lengths of the diagonals of a quadrilateral is less than or equal to the sum of the products of the opposite sides of the quadrilateral.
Gauss theorem
If in a quadrilateral two pairs of opposite sides are not parallel, then the two midpoints of its diagonals lie on a straight line
that passes through the midpoint of the segment connecting the two intersection points of the diagonals
and the intersection point of these two pairs of opposite sides.
Bretschneider ratio
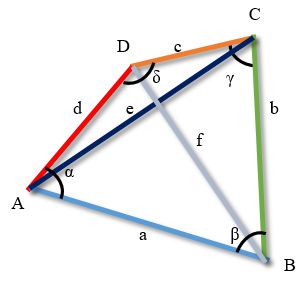
The product of the squares of the diagonals of an arbitrary non-self-intersecting quadrilateral
is equal to the sum of the products of the squares of its opposite sides
minus twice the product of all its sides times the cosine of the sum of the two opposite angles.
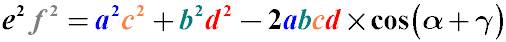
Euler formula
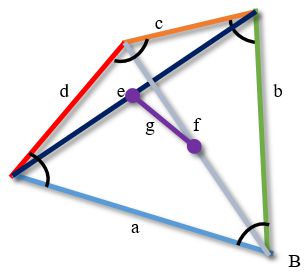
The square of the double distance between the midpoints of the diagonals
of an arbitrary non-self-intersecting quadrilateral is equal to the sum of the squares
of its sides minus the sum of the squares of its diagonals
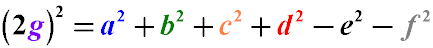
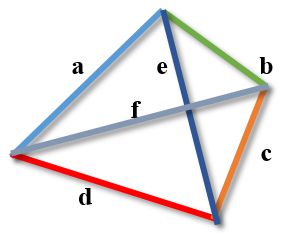
Middle lines of the quadrilateral
Each quadrilateral has three middle lines.
The midlines of a non-self-intersecting quadrilateral are the segments connecting the midpoints
of its opposite sides (first and second) and the segment connecting the midpoints of its diagonals.
In the figure, the middle lines of the quadrilateral are marked with dotted lines.
Quadrilateral centroid
The centroid of a quadrilateral is the intersection point of all its midlines.
Generalized Newton's theorem
The midlines of a non-self-intersecting quadrilateral formed by the midpoints of opposite sides (the first and second midlines) and the segment connecting the midpoints of the diagonals (the third midline) intersect at one point and bisect it.
The line passing through the midpoints of the diagonals of a quadrilateral and its centroid is also called Newton's line.
(see picture above)
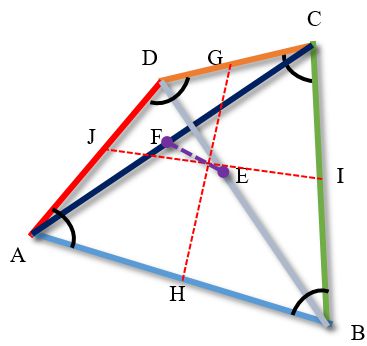
Varignon's theorem
The quadrilaterals formed by the line segments connecting the midpoints of opposite sides (GIHJ),
as well as the midpoints of the diagonals of the quadrilateral and the midpoints of opposite sides (EHFG, JEIF) are parallelograms.
These parallelograms are called Varignon parallelograms.
The quadrilateral formed by the midpoints of the opposite sides
(indicated by the dotted line GIHJ in the figure) is called the great parallelogram of Varignon.
- The centers of all three Varignon parallelograms lie in the middle of the segment connecting the midpoints of the sides of the original quadrilateral (at the same point, the segments connecting the midpoints of the opposite sides - the diagonals of the Varignon parallelogram) intersect.
- The perimeter of the large Varignon parallelogram is equal to the sum of the diagonals of the original quadrilateral.
- The area of the large Varignon parallelogram is equal to half the area of the original quadrilateral
- The area of the original quadrilateral is equal to the product of the first and second midlines of the quadrilateral and the sine of the angle between them
- The sum of the squares of the three middle lines of a quadrangle is equal to a quarter of the sum of the squares of all its sides and diagonals
Isosceles triangle |
Описание курса
| Existence of a quadrilateral with given sides
|

