Universal Formulas for Calculating the Area of an Arbitrary Triangle

Below are the formulas for finding the area of an arbitrary triangle that are suitable for finding the area of any triangle, regardless of its properties, angles,
or dimensions. The formulas are presented in the form of a picture, and explanations are provided for their application or justification of their correctness.
Additionally, a separate figure shows the correspondences of the letter symbols in the formulas and the graphic symbols on the drawing.

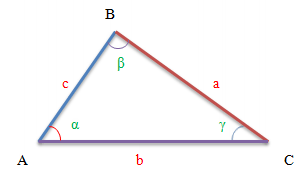
Explanations of the Formulas:

• a, b, c: Lengths of the sides of the triangle whose area we want to find.
• r: Radius of the circle inscribed in the triangle.
• R: Radius of the circle circumscribed around the triangle.
• h: Height of the triangle dropped by the side.
• p: Semiperimeter of the triangle, which is half the sum of its sides (perimeter).
• α: Angle opposite to side a of the triangle.
• β: Angle opposite to side b of the triangle.
• γ: Angle opposite to side c of the triangle.
• ha, hb, hc: Heights of the triangle dropped by the sides a, b, and c, respectively.

Please note that the given notations correspond to the figure above, so that when solving a real geometry problem, it would be visually easier for you
to substitute the correct values in the right places of the formula.

Formulas and Their Explanations:

1. Formula 1: The area of a triangle is equal to half the product of the height of the triangle and the length of the side to which this height is dropped.
   • Explanation: The height dropped onto the base will divide an arbitrary triangle into two right-angled triangles. If each of them is built up to
     a rectangle with dimensions b and h, then, obviously, the area of these triangles will be equal to exactly half the area of the rectangle
     (S = 1/2 * b * h).
2. Formula 2: The area of a triangle is equal to half the product of its two sides by the sine of the angle between them.
   • Explanation: Although it seems different from the previous one, it can easily be transformed into it. If we drop the height from angle B to
     side b, it turns out that the product of side a and the sine of angle γ, according to the properties of sine in a right triangle, is equal to the
     height of the triangle that we have drawn, which will give us the previous formula.
3. Formula 3: The area of an arbitrary triangle can be found by multiplying half the radius of the circle inscribed in it by the sum of the lengths of
   all its sides.
   • Explanation: In simpler terms, you need to multiply the semiperimeter of the triangle by the radius of the inscribed circle (this is easier
     to remember).
4. Formula 4: The area of an arbitrary triangle can be found by dividing the product of all its sides by 4 times the radius of the circle circumscribed
   around it.
5. Formula 5: Finding the area of a triangle through the lengths of its sides and its semiperimeter (half the sum of all its sides).
6. Heron's Formula (Formula 6): A representation of the same formula without using the concept of semiperimeter, only through the lengths of
   the sides.
7. Formula 7: The area of an arbitrary triangle is equal to the product of the square of the side of the triangle by the sines of the sides adjacent to it,
   divided by the double sine of the angle opposite to this side.
8. Formula 8: The area of an arbitrary triangle can be found as the product of two squares of the circle circumscribed around it and the sines of each
   of its angles.
9. Formula 9: If the length of one side and the values of two adjacent angles are known, then the area of the triangle can be found as the square
   of this side divided by the double sum of the cotangents of these angles.
10. Formula 10: If only the length of each of the heights of the triangle is known, then the area of such a triangle is inversely proportional to the lengths
    of these heights, as per Heron's Formula.
11. Formula 11: Allows you to calculate the area of a triangle based on the coordinates of its vertices, which are given as values (x, y) for each of the
    vertices. Please note that the resulting value must be taken modulo, since the coordinates of individual (or even all) vertices may be in the range
    of negative values.