Problem 1

In a regular triangular pyramid, the lateral faces are inclined to the base at an angle of 60°.
The distance from the center of the base to a lateral face is 2√3.
Find the volume of the pyramid.

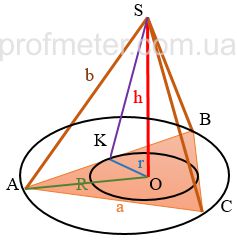
Solution:

1. Center of the equilateral triangle at the base:

In a regular triangular pyramid, the center of the base (the center of the inscribed circle of the equilateral triangle) coincides with the intersection
point of its medians.

Let the side length of the equilateral triangle at the base be aa. The distance from the center of the base to the lateral face is the radius of the circle
inscribed in the triangle, given by the formula:




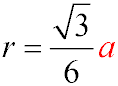
According to the problem, this distance is 2√3. Hence:

a √3 / 6 = 2√3.

Solve for a:

a = 12.

Thus, the side length of the base is a = 12.

2. Height of the pyramid (H):

A lateral face is an isosceles triangle with a base of length aa and a height drawn from the apex of the pyramid.
The height of the pyramid h forms an angle of 60° with the base plane.

Using the trigonometric relation:

h = r⋅tan⁡(60°).

Substitute r = 2√3 and tan⁡(60∘)=√3:

h = 2√3⋅√3 = 6.

Therefore, the height of the pyramid is h = 6.

3. Area of the base S_base:

The base of the pyramid is an equilateral triangle with a side length of a = 12. The area of an equilateral triangle is calculated as:

.

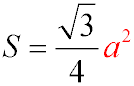Substitute a = 12:

S = 12² * √3 / 4 = 144 √3 / 4 = 36 √3.


4. Volume of the pyramid (V):

The volume of the pyramid is determined using the formula:

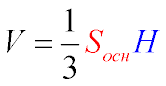
Substitute S_base=36√3 and H = 6:

Problem

The side of the base of a regular triangular pyramid is a, and the lateral edge is b. Find the volume of the pyramid.

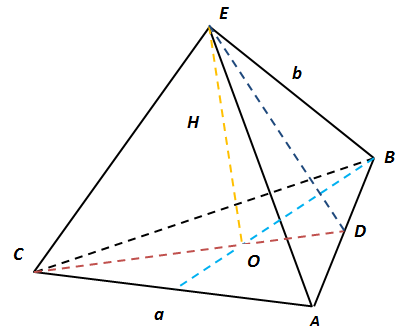
Solution

A regular triangular pyramid (tetrahedron) with a height, an apothem, and the height of the base.

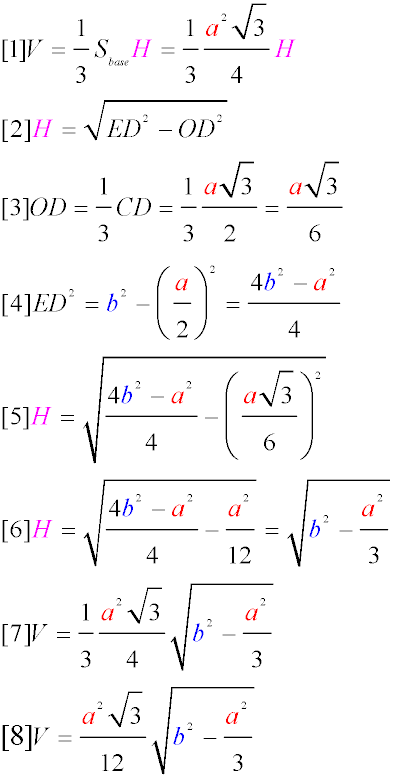
In the standard formula for the volume of a pyramid, we express the area of the base using the formula for the area of an equilateral triangle,
since we know its side. (Formula 1)

We find the height of the pyramid by expressing it using the Pythagorean theorem through the triangle OED as the difference of the squares
of the apothem ED and the segment to the point of intersection of the heights OD. (Formula 2)

We find OD using the property of an equilateral triangle. The point of intersection of the heights, medians, and angle bisectors is divided in
the ratio 1 to 2, which means it is equal to one-third of the height of the equilateral triangle. Substituting the formula for finding the height of an
equilateral triangle, we obtain the length of the desired segment OD, expressed through the side of the base of the pyramid. (Formula 3)

ED is the height of an isosceles triangle, which is easy to find, knowing the length of the base and the lengths of the lateral sides (given in the
problem statement). We also express it using the Pythagorean theorem. (Formula 4)

We substitute the values found in Formulas 3 and 4 into Formula 2, resulting in Formula 5.

We simplify the expression obtained in Formula 5 by expanding the brackets, bringing the fraction to a common denominator, and then simplifying
the expression again. We obtain Formula 6, which represents the height of the pyramid, expressed through the side of the base and the length of
the lateral edge, according to the given data.

In Formula 1, we substitute the found value of the height of the pyramid from Formula 6, resulting in Formula 7. We simplify it and obtain
the answer - Formula 8.