Problem 1: Find the Area Given Two Sides and the Angle Between Them

Problem: The sides of a triangle are 5 and 6 cm. The angle between them is 60 degrees. Find the area of the triangle.

Solution:

To solve this problem, we use the formula for the area of a triangle given two sides and the included angle:

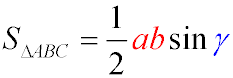
Given:

• a = 5 cm
• b = 6 cm
• γ=60°

Substitute the values into the formula:

Using the trigonometric value:

So,

Answer: 15√3 / 2

Problem 2: Find the Area of an Equilateral Triangle

Problem: Find the area of an equilateral triangle with a side of 3 cm.

Solution:

The area of an equilateral triangle can be found using the formula:

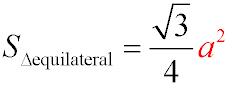
Given:

• a = 3 cm

Substitute the value into the formula:

Answer: 9√3 / 4 square cm.

Problem 3: Change in Area When Changing the Length of the Sides

Problem: How many times will the area of a triangle increase if the sides are increased by 4 times?

Solution:

Let's assume the original sides of the triangle are a, b, and c. The area of the original triangle can be found using Heron's formula:

If the sides are increased by 4 times, the new sides will be 4a, 4b, and 4c. The area of the new triangle will be:

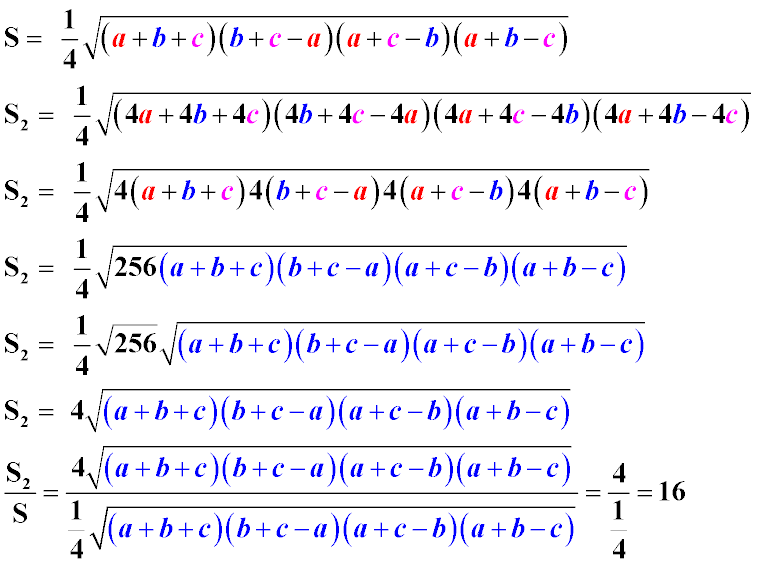
Answer: The area of the triangle will increase by 16 times.