Prism

This section is devoted to solving problems about prisms. For successful mastering of this section, it is necessary to take into account the following.

Prism definition

A prism is a three-dimensional polyhedron, two of whose faces are equal (identical) polygons lying in parallel planes, and the remaining faces are parallelograms, the opposite faces of these parallelograms are common with the corresponding sides of the parallel polygons.

Below, the figure shows a triangular, quadrilateral, and oblique quadrilateral prism. Usually (but not necessarily) to simplify the understanding of the relative position of the bases and their sides, the designations of the lower base begin with the Latin letters A, B, C, and so on, and the corresponding sides of the upper base are denoted by the same letters with the addition of one - A1, B1, C1, etc.

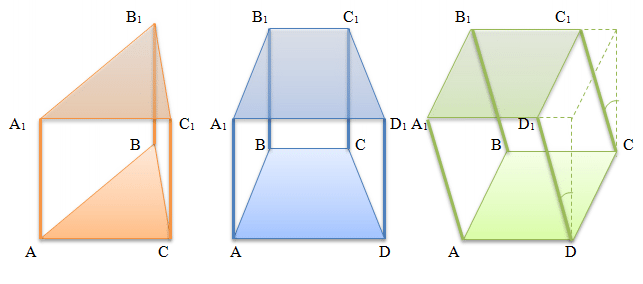
Other definitions of prism:

A prism is a polyhedron whose bases are equal polygons, the corresponding side faces of which are parallelograms.

Prism parts definitions:

Equal polygons lying in parallel planes are called the bases of the prism.

The faces of a prism connecting its prism bases (ABCD and A1B1C1D1) are called side faces.

The area (union, set) of all side faces of the prism is called the side surface.

Common faces of parallelograms connecting the bases of a prism are called lateral edges. (AA1 BB1 CC1 etc.)

The length of the segment connecting the bases of the prism and perpendicular to both bases at the same time is (called) the height of the prism.

A segment drawn between two vertices of a polyhedron, which is a prism, so that it does not belong to any plane of the prism (bases or side faces) is called the diagonal of the prism. (AC1)

The plane passes through the lateral edge of the prism and the diagonal of the base (not to be confused with the diagonal of the prism!) Is called the diagonal plane. (AA1C1C)

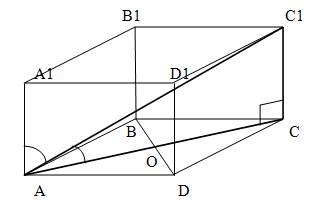
Prism Properties

• The bases of the prism are equal
• Each of the side faces is necessarily a parallelogram
• The side edges of the prism are parallel and equal to each other
• The side faces of a regular prism are equal rectangles
• At the intersection of a prism and a diagonal plane, the section is a parallelogram
• Perpendicular section perpendicular to all side edges of the prism
• The angles of a perpendicular section are the linear angles of the dihedral angles at the corresponding side edges
• Perpendicular section perpendicular to all side faces

Special cases of prisms

A parallelepiped is a prism whose base is a parallelogram.

A cuboid is a right prism whose base is a rectangle and all faces are rectangles.

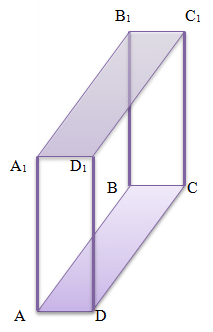
Straight prism - a prism in which the side edges are perpendicular to the plane of the base.

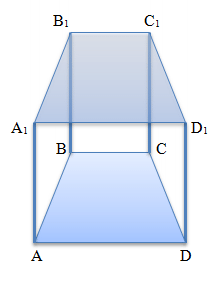
A regular prism is a straight prism whose bases are a regular polygon. (see also - regular quadrangular prism)

A cube is a regular prism, all sides of which are a regular quadrilateral (square)

Prism Volume

The formula for finding the volume of a prism is as follows:

V = Sh, where

V - prism volume

S - the base area of the prism

h - prism height

The total surface area of a prism is equal to the sum of its lateral surface area and twice the base area.

The area of the side surface of an arbitrary prism S=P x l, where P is the perimeter of the perpendicular section, and l is the length of the side rib.

The area of the side surface of a straight prism S=P x h, where P is the perimeter of the base of the prism, and h is the height of the prism.