Tetrahedron

Basic Concepts and Properties

A tetrahedron is a regular polyhedron (a regular triangular pyramid) where all faces are equilateral triangles.

Characteristics of a Tetrahedron:

• All faces are equal.
• It has 4 faces, 4 vertices, and 6 edges.
• All dihedral angles at the edges and all trihedral angles at the vertices are equal.

Elements of a Tetrahedron:

• Median of a Tetrahedron: This is a segment connecting a vertex with the point of intersection of the medians of the opposite face
  (medians of the equilateral triangle opposite the vertex).
• Bimedian of a Tetrahedron: This is a segment connecting the midpoints of skew edges (connecting the midpoints of the sides of the
  triangle, which is one of the faces of the tetrahedron).
• Height of a Tetrahedron: This is a segment connecting a vertex with a point on the opposite face and perpendicular to this face
  (i.e., it is the height drawn from any face and also coincides with the center of the circumscribed circle).

Properties of a Tetrahedron:

• All medians and bimedians of a tetrahedron intersect at one point.
• This point divides the medians in a ratio of 3:1, counting from the vertex.
• This point divides the bimedians in half.

Additional Properties of a Regular Tetrahedron:

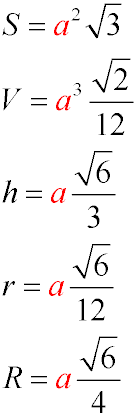
• a is the edge length of the tetrahedron
• h is the height of the tetrahedron (Formula 3)
• r - Radius of the Inscribed Sphere: The inscribed sphere touches all faces of the tetrahedron at their centers. The radius of the inscribed
  sphere can be found using the formula 4
• R - Radius of the Circumscribed Sphere: The circumscribed sphere passes through all vertices of the tetrahedron. The radius of the circumscribed
  sphere can be found using the formula 5
• S - Surface Area: The surface area of the tetrahedron can be found using the formula 1.
• V - Volume: The volume of the tetrahedron can be found using the formula 2

Applications of the Tetrahedron:

The tetrahedron has wide applications in various fields of science and technology. For example, in chemistry, the tetrahedral structure is the basis for many
molecules, such as methane (CH₄). In mathematics and geometry, the tetrahedron is used to study the properties of polyhedra and their symmetries. In
physics, tetrahedral structures are found in the crystal lattices of some materials.

Practical Examples

Note: This is part of a lesson with geometry problems (section on stereometry, pyramid problems). If you need to solve a geometry problem that is
not listed here, please write about it in the forum. In the problems, the symbol "square root" is denoted by "√".

Problem 1:

Find the surface area of a triangular pyramid where each edge is equal to √3.

Solution: Since all edges of the triangular pyramid are equal, it is a regular pyramid.
The surface area of a regular triangular pyramid is given by S=a²√3.

Given a=√3

Answer: 3√3

Problem 2:

All edges of a regular triangular pyramid are 4 cm. Find the volume of the pyramid.

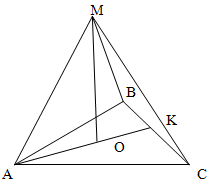
Solution: In a regular triangular pyramid, the height of the pyramid projects to the center of the base,
which is also the center of the circumscribed circle.

The radius R of the circumscribed circle is given by:

Given a = 4:

The height OM of the pyramid can be found from the right triangle AOM:

The volume V of the pyramid is given by:

The area S of the base is:

Given a = 4:

Thus:

Answer: 16 √2 / 3 cm³