Trigonometric Circle

A trigonometric circle is a circle with a unit radius and a center at the origin of the coordinate axes. Each point on this circle forms
a triangle with the following points:

• The origin of the coordinate axes (point (0, 0))
• A point on the circle (selected by us)
• A point on the X-axis, which is the projection of the selected point onto this axis (perpendicular to the X-axis)

Change in the Value of the Sine of the Angle Depending on Its Magnitude

As you can see, such a triangle is right-angled, since a perpendicular is always dropped from the selected point onto the abscissa axis.
The side connecting the origin of the coordinates and the selected point on the trigonometric circle (designated as B, B1, B2, B3 in
the figure) is always the hypotenuse of a right-angled triangle. The projection of the selected point is the leg, and the side from the point
of intersection with the X-axis forms the second leg.

The angle formed between the abscissa axis (X-axis) and the hypotenuse of the triangle is the angle for which the values of trigonometric
functions are calculated. This angle is measured from the positive direction of the abscissa axis (X-axis) as zero, then counterclockwise.
Thus, a full circle is 360 degrees or 2π radians.

To calculate the value of a trigonometric function for a selected angle of the trigonometric circle, it is enough to use the coordinates of
a point belonging to the circumference of the trigonometric circle. The figure above shows the calculation of the sine value for all angles.

For example, sin⁡α\sin \alpha for triangle OBC (where the coordinates of point B are (x, y)) will be equal to:

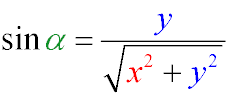
Properties of the Trigonometric Circle

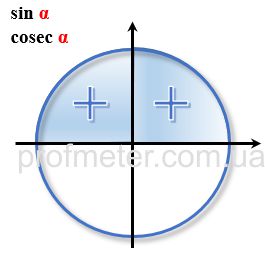
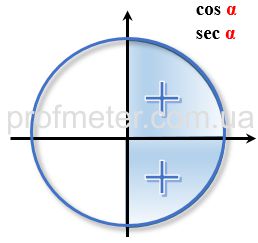
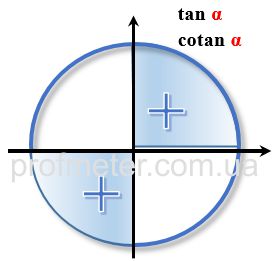
If we sequentially calculate the values of trigonometric functions for the trigonometric circle, it becomes clear that the result of such
calculations changes its sign depending on which quarter of the trigonometric circle the point is selected in. In this case, the sign of
the trigonometric function within the same quarter is preserved.

Signs of Trigonometric Functions in Coordinate Quarters in the Trigonometric Circle

Converting Angles Greater Than 360 Degrees or 2π Radians

When dealing with angles greater than 360 degrees or 2π radians, it's important to understand that these angles essentially "wrap around" the circle.
This means that after the angle value exceeds 360 degrees (or 2π radians), the result of calculating the trigonometric function will be the same as if
the angle were within the range of 0 to 360 degrees (or 0 to 2π radians).

Steps to Normalize the Angle

To bring the angle value to a "normal" range (i.e., between 0 and 360 degrees or 0 and 2π radians), follow these steps:

1. Subtract 360 Degrees or 2π Radians: From the given angle, subtract 360 degrees (or 2π radians) to reduce the angle.
2. Repeat the Operation: Continue subtracting 360 degrees (or 2π radians) as many times as necessary until the result is less than 360 degrees
   (or 2π radians).

Example

Let's say you have an angle of 450 degrees. To normalize this angle:

• Subtract 360 degrees:

The normalized angle is 90 degrees.

Similarly, for an angle of 5π radians:

• Subtract 2π radians:

• Subtract 2π radians again:

The normalized angle is π radians.

Why This Works

This process works because the trigonometric functions are periodic, meaning they repeat their values in regular intervals. For sine and cosine functions,
this interval is 360 degrees or 2π radians. Therefore, any angle that exceeds this interval can be reduced to an equivalent angle within the interval, and
the trigonometric function values will remain the same.