Axiom 3. PROPERTIES OF MEASURING SEGMENTS

Each segment has a certain length, greater than zero. The length of a segment is equal to the sum of the lengths of the parts to which it is divided by any of its points.

This statement is an axiom, that is, it is initially accepted as true and can not be proved.

Comment

We take the line a and denote by it the points A and B, which form the segment AB belonging to this line. Since the points A and B do not coincide, the length of the segment AB is greater than zero. The

If on a segment to take any point, except the start and end points of the segment, then the segment is divided by this point into two segments and its length is equal to the sum of the lengths of these segments.
Between points A and B we denote the point C, which breaks the segment AB into two parts - AC and CB.

The length of the segment AB is equal to the sum of the lengths of the segments AC and CB:

AB = AC + CB

This is the statement of the axiom



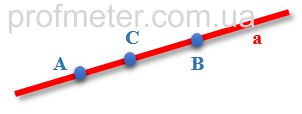AB = AC + CB

A line with points and segments marked on it
The length of each of the resulting segments is equal to the difference in the lengths of the whole segment (AB) and its second part (CB or AC).

AC = AB-CB and CB = AB-AC

On the basis of the assertion of this axiom, proof of the majority of theorems of planimetry and stereometry is constructed.