Angle: Definition and Properties

Definition of an Angle

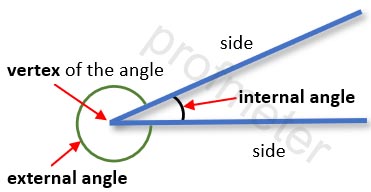
An angle is a geometric figure formed by two rays emanating from a common point. This common point is called the vertex of the angle, and the rays
are called the sides of the angle. The part of the plane that is located between the rays is called the interior of the angle.

An angle is a part of the plane delimited by two rays emanating from one point. It is a geometric figure that has a vertex, sides, and its own degree measure.

The plane is divided into two parts by the sides of the angle. The smaller of the angles is called the internal angle, and the larger is the external angle.
To avoid different interpretations of which angle is being discussed, its sides are often connected by an arc on the drawing.

Angular Measure of an Angle

An angular measure has the following properties:

• Equal angles correspond to an equal angular measure.
• A smaller angle corresponds to a smaller angular measure.
• For an angle whose sides coincide (zero angle), the angular measure is zero (the same is true for the angle between parallel lines).
• Each non-zero angle has a certain angular measure greater than zero.
• (Additivity) The angular measure of an angle is equal to the sum of the angular measures of the angles into which it is divided by any ray passing
  between its sides.

An angle is measured in degrees, radians, grades, and revolutions.

1 turnover = 360 degrees = 2π radians = 400 grades

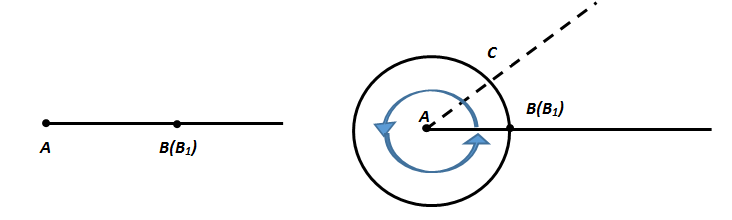
Let's consider an angle whose sides coincide (∠ВАВ₁). Its degree measure is 0°.

If one side of the angle (AB) is fixed and the second side (AB₁) is rotated counterclockwise until it coincides with the first side (AB), then the plane of such
an angle will form a full angle. Therefore, angle A (designated as ∠A) is a full angle.

Properties of an Angle and Its Degree Measure

1. Equal Angles: Equal angles have the same angular measure.
2. Zero Angle: An angle whose sides coincide has an angular measure of zero.
3. Full Angle: A full angle is formed when one side of the angle is rotated 360 degrees around the vertex to coincide with the other side. Its measure
   is 360°.
4. Straight Angle: Half of a full angle is a straight angle, which measures 180°.

Designation of Angles

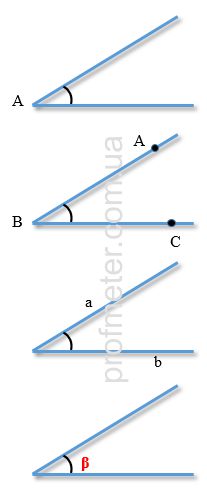
Angles can be designated in various ways in geometric drawings and diagrams:

1. Single Letter: An angle can be designated as a combination of the sign of the angle and its vertex, for example, ∠A.
2. Three Letters: An angle can also be designated using three capital letters. For example, ∠ABC is an angle with vertex B, the sides of which are
   rays BA and BC.
3. Angle Symbol with Sides: An angle can be designated using the angle symbol and the sides of the angle, for example, ∠ab.
4. Greek Letters: An angle can be designated by Greek letters α, β, γ, etc. The only exception is the letter "π", which is not used to designate
   angles.

Degree Measure of an Angle

If you take a full angle and divide it into 360 parts, then each part, which is 1/360 of the full angle, is called a degree (denoted as 1°).

Therefore, the full angle is 1° * 360 = 360°.

Half of the full angle makes up a straight angle, which is 360° / 2 = 180°.

Central and Inscribed Angles in a Circle

A central angle is an angle whose vertex coincides with the center of the circle. The degree measure (magnitude) of such an angle is equal to the degree
measure of the arc of the circle enclosed between the sides of the angle.

An inscribed angle is an angle whose vertex lies on a circle and whose sides intersect it. The size of such an angle is equal to half the angular measure
of the arc of the circle that is enclosed between its sides.

Properties of Angles Inscribed in a Circle

1. Inscribed angles that rest on the same arc of the circle are equal.

2. The size of an inscribed angle that rests on the same arc of the circle as the central angle is equal to half the size of such a central angle.