The Concept of a Polygon

A polygon is a geometric figure that consists of a closed broken line. There are three common ways to define a polygon:

1. A polygon is a flat, closed broken line.
2. A polygon is a flat, closed broken line without self-intersections.
3. A polygon is a part of a plane that is bounded by a closed broken line.

The vertices of the broken line are called the vertices of the polygon, and the segments between the vertices are called the sides of the polygon.

Key Terms and Definitions

• Adjacent Vertices: Vertices of a polygon are called adjacent if they are the endpoints of one of its sides.
• Diagonals: Segments connecting non-adjacent vertices of a polygon are called diagonals.
• Interior Angle: The angle at a given vertex formed by the sides converging at that vertex and located inside the polygon.
• Exterior Angle: For a convex polygon, the exterior angle at a given vertex is the angle adjacent to the interior angle at that vertex.
  In general, an exterior angle is the difference between 180° and the interior angle.

Types of Polygons

• Convex Polygon: A polygon is called convex if any of the following conditions are true:

  • The polygon lies entirely on one side of any line connecting its adjacent vertices.
  • The polygon is the intersection of several half-planes.
  • Any segment with endpoints at points belonging to the polygon lies entirely within the polygon.

• Regular Polygon: A convex polygon is called regular if all its sides and angles are equal. Examples include an equilateral triangle,
  a square, and a regular pentagon.

• Inscribed Polygon: A convex polygon is called inscribed in a circle if all its vertices lie on the circumference of the circle.

• Circumscribed Polygon: A convex polygon is called circumscribed about a circle if all its sides are tangent to the circle.

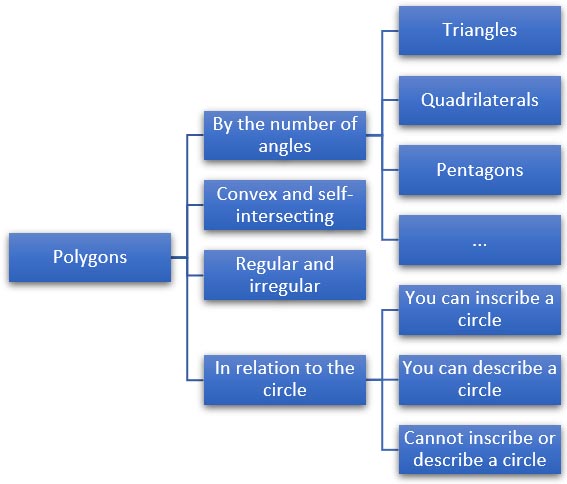
Classification (types) of polygons

Classification of Polygons

Polygons can be classified by various properties, the most important of which are:

1. Number of Vertices:

   • A polygon with three vertices is called a triangle.
   • A polygon with four vertices is called a quadrilateral.
   • This naming continues based on the number of vertices (e.g., pentagon for five vertices, hexagon for six, etc.).

2. Convexity:

   • A convex polygon always lies on one side of a line that contains any of its sides. This means all interior angles are less than 180°.

3. Regularity:

   • A regular polygon has all sides and angles equal. Examples include an equilateral triangle and a square.
     Regular polygons have special properties due to their symmetry.

4. Ability to Inscribe or Circumscribe a Circle:

   • Polygons can be distinguished by their ability to have a circle inscribed within them (all sides tangent to the circle)
     or circumscribed around them (all vertices lie on the circle). For example, it is always possible to circumscribe a circle
     around any triangle.

Properties of Polygons

• Interior Angles:

  • The sum of the interior angles of an ( n )-gon is ((n - 2)* 180°).
  • For a regular ( n )-gon, each interior angle is ( (n - 2) * 180° ) / n.

• Diagonals:

  • The number of diagonals in any polygon is given by the formula ( n(n - 3) ) / 2, where ( n ) is the number of sides.

Special Types of Polygons

• Self-Intersecting Polygons:

  • These polygons can also be regular. An example is a pentagram (a five-pointed star).

• Convex Polygons:

  • A convex polygon is one where any line segment drawn between two points inside the polygon lies entirely within the polygon.

• Regular Polygons:

  • These polygons have equal sides and angles. Examples include the equilateral triangle, square, and regular pentagon.

Examples

• Triangle: A three-sided polygon.
• Quadrilateral: A four-sided polygon.
• Pentagon: A five-sided polygon.
• Hexagon: A six-sided polygon.