|
|
Volume of a Prism with a Right-Angled Triangle at the Base
A prism with a right-angled triangle at the base can have its volume calculated using various formulas based on the lengths of the sides of the right triangle,
its angles, and the radii of the inscribed or circumscribed circles.
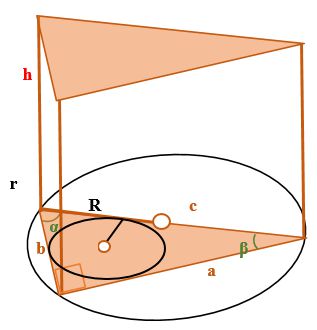
Formulas for Calculating the Volume of a Prism with a Right Triangle at the Base
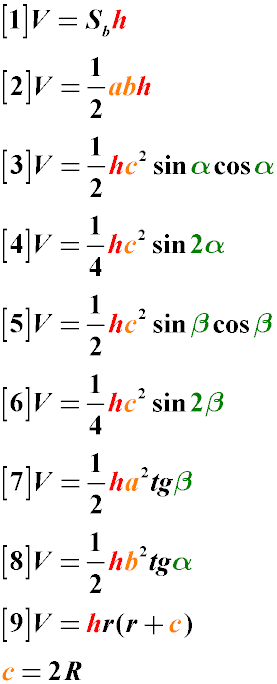
where:
- V is the volume of the prism,
- a and b are the legs of the right triangle,
- c is the hypotenuse of the right triangle,
- α is the angle opposite the leg a
- h is the height of the prism
- β is the angle opposite the leg b
- r is the radius of the circle inscribed in the base of the prism
- Volume through the Legs of the Right Triangle: The volume of a prism with a right triangle at the base can be calculated as half the product of
the legs times the height (Formula 2)
- Volume through the Hypotenuse and Angles: The volume of a prism with a right triangle at the base can be calculated as half the square of
the hypotenuse times the sine of angle α times the cosine of angle α times the height of the prism (Formula 3)
- Volume through the Hypotenuse and Double Angle: The volume of a prism with a right triangle at the base can be calculated as the product
of one-fourth of the square of the hypotenuse by the sine of double angle α and by the height of the prism (Formula 4)
- Volume through the Hypotenuse and Other Angle: The volume of a prism with a right triangle at the base can be calculated as the product
of half the square of the hypotenuse times the sine of angle β times the cosine of angle β times the height of the prism (Formula 5)
- Volume through the Hypotenuse and Double Angle: The volume of a prism with a right triangle at the base can be calculated as the product
of one-fourth of the square of the hypotenuse times the sine of double angle β times the height of the prism (Formula 6)
- Volume through the Leg and Tangent of the Adjacent Angle: The volume of a prism with a right triangle at the base can be found as half the
square of the leg multiplied by the tangent of the adjacent acute angle and multiplied by the height of the prism (Formula 7)
- Volume through the Radius of the Inscribed Circle: The volume of a prism with a right triangle as its base can be found as the product of
the height of the prism, the radius of the inscribed circle, multiplied by the sum of the radius of the inscribed circle and the hypotenuse (Fomula 8)
Additional Note
If a circle is circumscribed around a right triangle, then the hypotenuse of the triangle lies on its diameter, i.e., c = 2R. Therefore, if necessary, you can
replace c in the formulas with 2R.
These formulas provide a comprehensive approach to calculating the volume of a prism with a right-angled triangle at its base using different geometric
properties.
Volume of a Regular Triangular Prism |
Описание курса
| Volume of a prism with an isosceles triangle at the base
|

