|
|
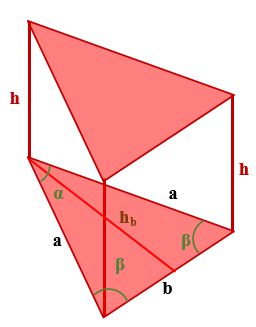
If the base of a prism is an isosceles triangle, you can use the following formulas to find its volume:
Formulas for Finding the Volume of a Prism with an Isosceles Triangle at the Base
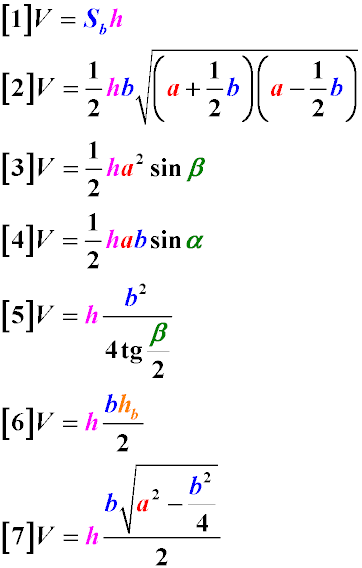
where:
- V is the volume of the prism,
- a is the length of one of the equal sides of the isosceles triangle,
- b is the base of the isosceles triangle,
- h is the height of the prism
- α is the angle between the sides and across the base of the isosceles triangle
- β is the angle between the side and the base of the isosceles triangle
- hb is the height of the isosceles triangle, dropped from its base
- Volume through the Dimensions of the Side and Base: The volume of a prism with an isosceles triangle at the base can be found
through the dimensions of the side, the base of the isosceles triangle, and the height of the prism (Formula 2)
- Volume through the Height of the Prism and the Side of the Base: The volume of a prism with an isosceles triangle at the base
can be found as half the product of the height of the prism by the square of the side of the base of the isosceles triangle and the sine
of the angle at the base of the isosceles triangle (Formula 3)
- Volume through the Height of the Prism and the Base of the Isosceles Triangle: The volume of a prism with an isosceles triangle
at the base can be calculated as half the product of the height of the prism by the size of the side of the isosceles triangle
and the size of the base of the isosceles triangle and the sine of the angle at the vertex of the isosceles triangle (Formula 4)
- Volume through the Height of the Prism and the Base of the Isosceles Triangle: The volume of a prism with an isosceles triangle
at the base can be calculated as the product of the height of the prism by the square of the base of the isosceles triangle and divided
by four tangents of half the angle at the base of the isosceles triangle (Formula 5)
- Volume through the Height of the Prism and the Height of the Isosceles Triangle: The volume of a prism with an isosceles triangle
at the base can be calculated as the product of half the height of the prism by the base of the isosceles triangle and the height of
the isosceles triangle dropped onto this base (Formula 6)
- Volume through the Height of the Prism and the Base of the Isosceles Triangle: The volume of a prism with an isosceles triangle
at the base can be calculated as the product of half the height of the prism by the base of the isosceles triangle, multiplied by the square
root of the difference of the squares of the side of the isosceles triangle and half the base of the isosceles triangle (Formula 7)
These formulas provide a comprehensive approach to calculating the volume of a prism with an isosceles triangle at its base using different
geometric properties.
Volume of a Prism with a Right-Angled Triangle at the Base |
Описание курса
| Rectangular Prism
|

