Volume of a Parallelepiped and a Cube

If the base of a right prism is a rectangle, then the number of formulas for finding the volume of such a prism will also be greater.
Right quadrilateral prisms, whose bases are quadrilaterals, include parallelepipeds and cubes.

Formulas for Finding the Volume of a Parallelepiped and a Cube

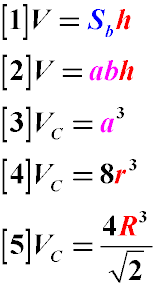
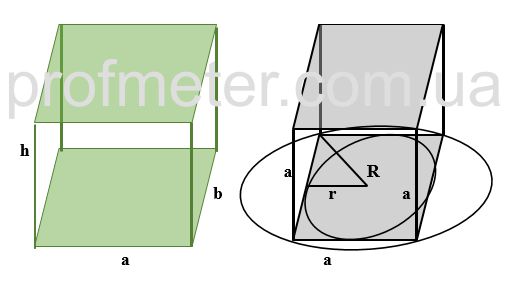
1. Volume of a Parallelepiped: The volume of a parallelepiped is equal to the product of the area of its base and its height. If the base is a rectangle
   with sides a and b, and the height is h, the volume V is given by Formula 2.
2. Volume of a Cube: The volume of a cube is equal to the cube of its side length. If the side length of the cube is a, the volume Vc is given by Formula 3.
3. Volume of a Cube Using the Radius of the Inscribed Circle: The volume of a cube can also be found using the radius of the circle inscribed in its base.
   If r is the radius of the inscribed circle, the volume Vc is given by Formula 4.
4. Volume of a Cube Using the Radius of the Circumscribed Circle: The volume of a cube can be found using the radius of the circle circumscribed
   around its base. If R is the radius of the circumscribed circle, the volume Vc is given by Formula 5.

Additional Explanations

• Parallelepiped: A parallelepiped is a six-faced figure (hexahedron) where each face is a parallelogram.
  The volume formula V=a×b×h applies to right parallelepipeds, where the height h is perpendicular to the base.

• Cube: A cube is a special case of a parallelepiped where all sides are equal. The formulas for the volume of a cube using the radii of the inscribed
  and circumscribed circles provide alternative methods for calculation based on geometric properties.

Examples

1. Parallelepiped Example: If a parallelepiped has a base with sides a = 4 cm and b = 5 cm, and a height h = 10 cm, the volume is:

V=4×5×10=200 cm³


2. Cube Example: If a cube has a side length a = 3 cm, the volume is:

Vc=3³=27 cm³


3. Cube Using Inscribed Circle: If the radius of the inscribed circle r = 1 cm, the volume is:

Vc=8×1³=8 cm³


4. Cube Using Circumscribed Circle: If the radius of the circumscribed circle R = 2 cm, the volume is:

These formulas and examples illustrate how to calculate the volume of parallelepipeds and cubes using different geometric properties.