Список предметов
Cylinder with inscribed prism problems
67 / 67
Note. This is part of the lesson with geometry problems (stereometry section). If you need to solve a geometry problem
that is not here, write about it in the forum.

Problem. Prism inscribed in a cylinder

A prism is inscribed in a cylinder. The base of the prism is a right triangle, the leg of which is 2a, and the adjacent angle
is 60 degrees. The diagonal of the larger lateral face of the prism makes an angle of 45 degrees with the plane of its base.

Find the volume of the cylinder.

Given Data:

  1. The base of the prism is a right triangle with one leg of length 2a and an adjacent angle of 60°.
  2. The diagonal of the larger lateral face of the prism makes an angle of 45° with the plane of its base.
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.

Step-by-Step Solution:

  • Determine the dimensions of the right triangle base:
    • The given leg is 2a.
    • The adjacent angle is 60°.

    Using trigonometry, we can find the other leg and the hypotenuse:

    • The other leg b can be found using the tangent function:
tan⁡(60°)=b / 2a
b = 2a ⋅ tan⁡(60°) = 2a√3
  • The hypotenuse cc can be found using the Pythagorean theorem:
The hypotenuse c can be found using the Pythagorean theorem

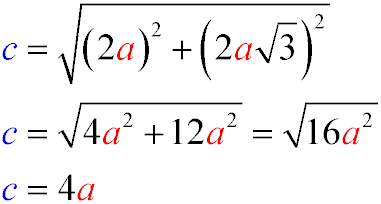
  • Determine the height of the prism:
    • The diagonal of the larger lateral face makes an angle of 45° with the plane of its base.
    • The larger lateral face is a rectangle with one side equal to the hypotenuse 4a and the other side equal to
      the height hh of the prism.
    • The diagonal d of this rectangle can be found using the Pythagorean theorem:
The diagonal d of this rectangle can be found using the Pythagorean theorem

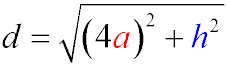
  • Given that the diagonal makes an angle of 45° with the base, we have:
tan⁡(45∘) = 1 = h / 4a ⟹ h=4a
  1. Determine the radius and height of the cylinder:
    • The cylinder circumscribes the prism, so the diameter of the cylinder is equal to the hypotenuse of the right triangle
      base of the prism.
    • Therefore, the radius R of the cylinder is:
R=c / 2=4a / 2=2a
  • The height HH of the cylinder is equal to the height of the prism:
H=4a
  • Calculate the volume of the cylinder:
    • The volume VV of the cylinder is given by:
The volume V of the cylinder is given by formula:

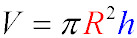
  • Substituting the values of R and h:
V=π(2a)2(4a)=π⋅4a2⋅4a=16πa3

Summary:

  • The volume of the cylinder is 16πa3 .

Problem

A regular hexagonal prism is inscribed in a cylinder. Find the angle between the diagonal of its lateral face and the axis of the
cylinder, if the radius of the base is equal to the height of the cylinder.

Solution

Let's solve the problem step by step with more details.

  1. Understanding the Problem:

    • We have a regular hexagonal prism inscribed in a cylinder.
    • The radius of the base of the cylinder is equal to the height of the cylinder.
    • We need to find the angle between the diagonal of the lateral face of the prism and the axis of the cylinder.

  2. Key Elements:

    • Radius of the Cylinder (r): This is also the radius of the base of the hexagonal prism.
    • Height of the Cylinder (h): Given that the radius is equal to the height, we have h=rh = r.
    • Side of the Hexagon (s): For a regular hexagon inscribed in a circle, the side length ss is equal to the radius
      of the circle, so s=rs = r.

  3. Lateral Face of the Prism:

    • The lateral face of the hexagonal prism is a rectangle.
    • One side of the rectangle is the height of the cylinder h=rh = r.
    • The other side of the rectangle is the side of the hexagon s=rs = r.

  4. Diagonal of the Lateral Face:

    • The diagonal of the lateral face forms a right-angled triangle with the height and the side of the hexagon.
    • The legs of this right-angled triangle are both equal to rr.

  5. Angle Between the Diagonal and the Axis:

    • The angle θ\theta between the diagonal of the lateral face and the axis of the cylinder can be found using the
      tangent function:
tan⁡(θ)=opposite / adjacent = r / r = 1
  • Therefore, θ=tan⁡−1(1)=45°.

Conclusion

The angle between the diagonal of the lateral face of the regular hexagonal prism and the axis of the cylinder is 45°.

0  


 Cylinder | Описание курса