|
|
Note: This is a lesson with solutions to geometry problems (stereometry section, regular pyramid with a quadrangle at the base).
If you need to solve a geometry problem that is not here - write about it in the forum.
In the problems, the "√" sign is used instead of the "square root" symbol.
Task
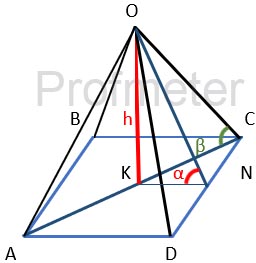
In a regular quadrilateral pyramid, the base side is aa, the height is 3a3a. Find the angles of inclination of the lateral edges and
the lateral faces to the plane of the base.
Solution
Let's find the angle of inclination of the edges to the plane of the base.
Since the base of a regular pyramid is a regular quadrilateral, in this case it is a square.
Since the height of the pyramid is projected to the center of the base, this is the point of intersection of the diagonals.
Whence KN = a/2
Triangle OKN is rectangular, OK is the height, equal to 3a.
Let's find the tangent of the angle KNO, denoting it as α.
tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°
Let's find the angle of inclination of the edge of the pyramid.
A regular quadrilateral pyramid has a square base, so the diagonal of the base can be
found by the formula:
d = AC = a√2
The diagonals are bisected at the intersection point.
Thus, for a right triangle OKC, the tangent of the angle KCO (denoted as β ) is
tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°
Answer: the angle of inclination of the faces arctg 6 ≈ 80.5377 °; the angle of inclination of the edges arctg 6/√2 ≈ 76.7373°
Problems about a regular quadrangular pyramid |
Описание курса
| With a triangle at the base
|

