Note: see also table of values of trigonometric functions of other angles.
Sine, cosine, tangent angle 45 degrees (sin 45, cos 45, tg 45)
Table values for sine 45, cosine 45, and 45 degree tangent are given below. The following is an explanation of the method and the correctness of the calculation of these values for an arbitrary rectangular triangle.
VALUE OF TRIGONOMETRIC FUNCTIONS AT α = 45 °
Let's create and consider a rectangular triangle ABC in which the angle ∠ B = 45 °. On the basis of the ratio of its sides, we calculate the value of trigonometric functions in a rectangular triangle for an angle of 45 degrees. Since the triangle is rectangular, the values of the sine, cosine and tangent functions will be equal to the ratio of its respective parties.
Since the values of sinus, cosine and tangent functions depend exclusively on the degree angle of the angle (or the value expressed in radians), the ratios found by us and will be the values of the sinus 45, cosine 45, and the tangent 45 degrees.
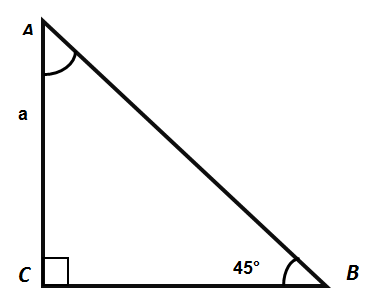
According to the properties of a rectangular triangle, the angle C is straight and is equal to 90 degrees. Angle B we originally built with a degree degree of 45 degrees. We find the value of the angle A. Since the sum of the angles of the triangle is 180 degrees, then
∠А + ∠В + ∠С = 180°
The angle C is straight and equal to 90 degrees, angle B we first defined as 45 degrees, thus:
∠А = 180° -∠С - ∠В = 180° - 90° - 45° = 45°,
Since in this triangle two angles are equal, then the triangle ABC is a rectangular, and, at the same time, an isosceles one, in which both cateches are equal: AC = BC.
Assume that the length of the sides is equal to some number of AS = BC = a.
Knowing the length of the coils, we calculate the length of the hypotenuse.
According to Pythagoras's theorem: АВ2=АС2+ВС2
Let's replace the lengths AC and BC with the variable a, then we obtain:
АВ2 = а2 + а2 = 2а2,
then AB = a√2.
As a result, we expressed the lengths of all sides of a rectangular triangle with an angle of 45 degrees through the variable a.
According to the properties of trigonometric functions in a rectangular triangle, the ratio of the corresponding sides of the triangle will be equal to the value of the corresponding functions. Thus for an angle α = 45 degrees:
sin α = BC / AB (according to the definition of a sinus for a rectangular triangle - this is the ratio of the opposite angle to the hypotenuse, BC - catheter, AB - hypotenuse)
cos α = AC / AB (according to the cosine definition - this is the ratio of the adjacent catheter to the hypotenuse, AC - catheter, AB - hypotenuse)
tg α = BC / AC (Similarly, the tangent for the angle α will be equal to the ratio of the opposing catheter to the adjacent)
Instead of designating the sides, we will substitute the values of their lengths through the variable a.
Proceeding from this (see table of values sin 45, cos 45, tg 45) we obtain:
The table values sin 45, cos 45, tg 45 (that is, the values of sinus 45, cosine 45, and 45 degree tangent can be calculated as the ratio of the corresponding sides of this triangle), we substitute the calculated values of the lengths of the sides in the formula and get the result in the image below.
Table values: sinus 45, cosine 45 and tangent 45 degrees
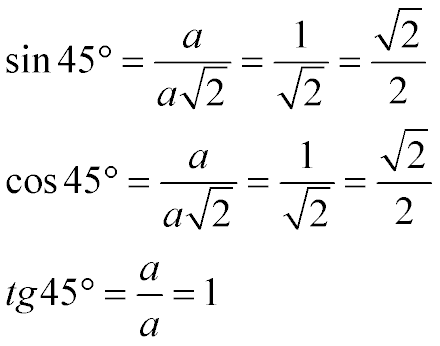
So:
-
45 degree tangent equals one
-
the sinus of 45 degrees is equal to the cosine of 45 degrees and is equal to the root of the two halves (the same as the unit divisible by the root of the two)
As can be seen from the calculations given above, to calculate the values of the corresponding trigonometric function, not the lengths of the sides of the triangle are important, but their ratio, which is always the same for the same angles, regardless of the size of a particular triangle.
Sine, cosine and tangent angle π / 4 radians
In the tasks proposed for solving in senior classes and tests, instead of the degree angle of the angle is often found indication of its magnitude, measured in radians. The degree of the angle, expressed in radians, is based on the number of pi, which expresses the dependence of the circumference of the circle to its diameter.
For ease of understanding, I recommend to remember the simple principle of translating degrees in radians. The diameter of the circle covers an arc which is 180 degrees. Thus, the PID will be 180 degrees. Where it is easy to list any degree of angle in the radians and back.
Let's take into account that the angle of 45 degrees, expressed in radians, is equal to (180/45 = 4) π / 4 (four to four). Therefore, the values found by us are true for the same degree angle of the angle expressed in radians:
-
tangent π / 4 (pi per four) is equal to one
-
sinus π / 4 (pi for four) degrees equals cosine π / 4 degrees and equals the root of two in half
For the convenience of visual perception, these values are shown in the figure below.
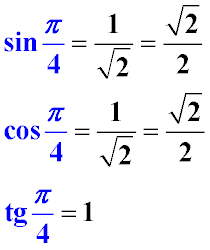
Note: see also table of values of trigonometric functions of other angles.

