|
|
The section contains problems in geometry (section planimetry) about trapezoids. If you did not find a solution to the problem - write about it on the forum. The course will be updated for sure.
Trapeze. Definition, formulas and properties
A trapezium (from other Greek ) is a quadrilateral with exactly one pair of opposite sides parallel.
A trapezoid is a quadrilateral with two opposite sides parallel.
Note. In this case, the parallelogram is a special case of a trapezoid.
The parallel opposite sides are called the bases of the trapezoid, and the other two are called the sides.
Trapezes are:
-
- versatile;
-
- isosceles;
-
- rectangular
. 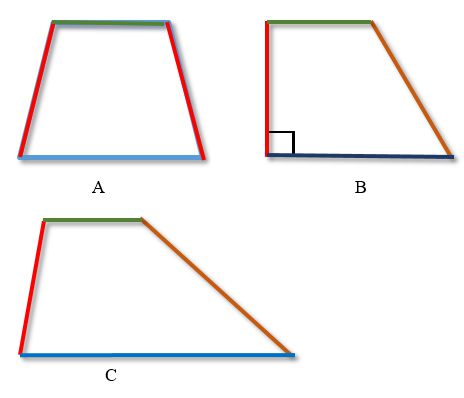
The sides are marked in red and brown, the bases of the trapezium are marked in green and blue.
A - isosceles (isosceles, isosceles) trapezoid
B - rectangular trapezoid
C - versatile trapezoid
A versatile trapezoid has all sides of different lengths, and the bases are parallel.
An isosceles trapezoid has equal sides and parallel bases.
A rectangular trapezoid has parallel bases, one side is perpendicular to the bases, and the other side is inclined to the bases.
Trapezoid Properties
- The median line of the trapezoid is parallel to the bases and equal to half their sum
- The segment connecting the midpoints of the diagonals is equal to half the difference of the bases and lies on the midline.
- Parallel lines intersecting the sides of any angle of the trapezoid cut off proportional segments from the sides of the angle (see Thales' theorem)
- The intersection point of the diagonals of a trapezoid, the intersection point of the extensions of its lateral sides and the midpoints of the bases lie on one straight line (see also the properties of a quadrilateral)
- Triangles lying on the bases of a trapezoid whose vertices are the point of intersection of its diagonals are similar. The ratio of the areas of such triangles is equal to the square of the ratio of the bases of the trapezoid
- Triangles lying on the sides of a trapezoid, the vertices of which are the point of intersection of its diagonals, are equal in area (equal in area)
- A circle can be inscribed in a trapezoid if the sum of the lengths of the bases of the trapezoid is equal to the sum of the lengths of its sides. The median line in this case is equal to the sum of the sides divided by 2 (since the median line of the trapezoid is equal to half the sum of the bases)
- The segment parallel to the bases and passing through the intersection point of the diagonals is divided by the latter in half and is equal to twice the product of the bases divided by their sum 2ab / (a + b) (Burakov's formula)
Trapeze angles
The angles of a trapezoid can be acute, straight and obtuse.
Only two angles can be straight.
A rectangular trapezoid has two right angles, and the other two are acute and obtuse.
Other types of trapezoids have: two acute angles and two obtuse ones.
The obtuse angles of a trapezoid belong to the shorter base, and the acute angles to the larger base.
Any trapezoid can be considered as a truncated triangle, in which the line of section is parallel to the base of the triangle.
Important. Please note that in this way (by additional construction of a trapezoid to a triangle)
some problems about a trapezoid can be solved and some theorems can be proved.
How to find the sides and diagonals of a trapezoid
Finding the sides and diagonals of a trapezoid is done using the formulas below.:
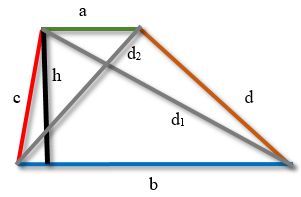
In these formulas, the notation is used, as in the figure.
a - the smallest of the bases of the trapezoid
b - the largest of the bases of the trapezoid
c,d - sides
h1h2 - diagonals
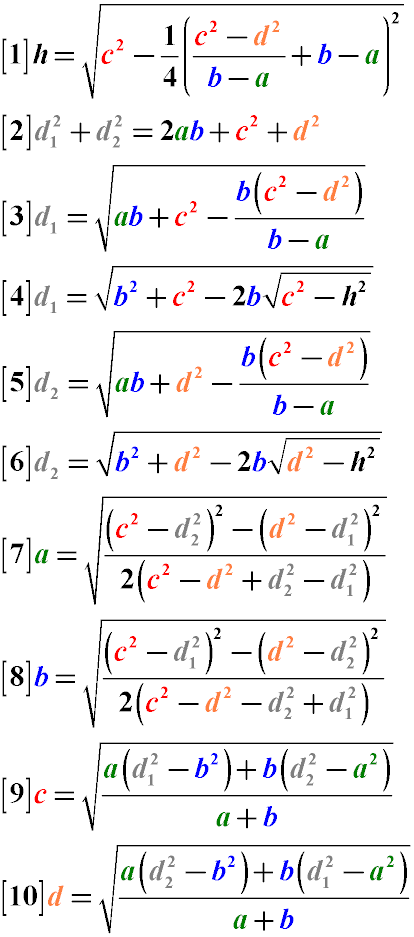
The sum of the squares of the diagonals of a trapezoid is equal to twice the product of the bases of the trapezoid plus the sum of the squares of the sides (Formula 2)
Trapezium area
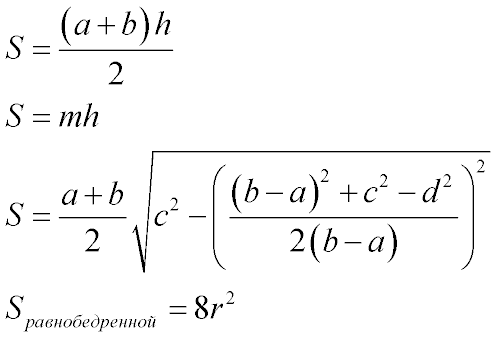
where
a and b are the parallel bases of the trapezoid
c and d - sides of the trapezoid
m - the middle line of the trapezoid
r- radius of the circle inscribed in the trapezoid
S - area of the trapezoid
Height of parallelogram |
Описание курса
| Diagonals of a trapezoid
|

