|
|
Regular Triangular Pyramid
A regular triangular pyramid is a pyramid whose base is a regular triangle, and whose apex is projected into the center of the base.
Elements of a Regular Triangular Pyramid
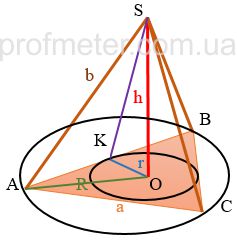
-
Base (ABC): The regular triangle at the base of the pyramid.
-
Height (OS): The perpendicular segment drawn from the apex of the pyramid to the plane of its base.
-
Apothem (KS): The height of a lateral face drawn from its apex.
-
Radius of the Inscribed Circle (OK): The radius of the circle inscribed in the base.
-
Radius of the Circumscribed Circle (AO): The radius of the circle circumscribed around the base.
-
Dihedral Angle (SKO): The angle between the base and the face of the pyramid. In a regular pyramid, these angles are equal.
Important Note
In a regular triangular pyramid, the length of an edge (AS, BS, CS) may not be equal to the length of the side of the base (AB, AC, BC).
If the length of the edge of a regular triangular pyramid is equal to the length of the side of the base, then such a pyramid is called
a tetrahedron (see below).
Properties of a Regular Triangular Pyramid
-
The lateral edges of a regular pyramid are equal.
-
All lateral faces of a regular pyramid are isosceles triangles.
-
A sphere can be inscribed in a regular triangular pyramid or circumscribed around it.
-
If the centers of the sphere inscribed and circumscribed around a regular triangular pyramid coincide, then the sum of the plane
angles at the apex of the pyramid is equal to π (180 degrees), and each of them is respectively equal to π / 3 (60 degrees).
-
The lateral surface area of a regular pyramid is equal to half the product of the perimeter of the base and the apothem.
-
The apex of the pyramid is projected onto the base at the center of a regular equilateral triangle, which is the center of the inscribed
circle and the intersection point of the medians.
Formulas for a Regular Triangular Pyramid
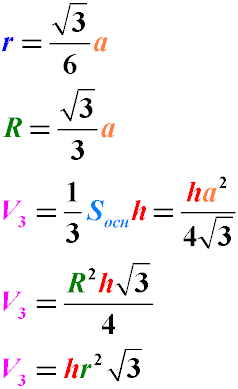
Where:
-
V is the volume of the regular pyramid.
-
h is the height of the pyramid.
-
a is the length of the side of the base.
-
R is the radius of the circumscribed circle.
-
r is the radius of the inscribed circle.
Since a regular triangular pyramid is a special case of a regular pyramid, the formulas that are true for a regular pyramid
are also true for a regular triangular one.
Tetrahedron
A special case of a regular triangular pyramid is a tetrahedron.
Definition
A tetrahedron is a regular polyhedron (regular triangular pyramid) in which all faces are regular triangles.
Properties of a Tetrahedron
-
All faces are equal.
-
It has 4 faces, 4 vertices, and 6 edges.
-
All dihedral angles at edges and all trihedral angles at vertices are equal.
-
The median of a tetrahedron is a segment connecting a vertex with the intersection point of the medians of the opposite face
(the medians of an equilateral triangle opposite the vertex).
-
The bimedian of a tetrahedron is a segment connecting the midpoints of the intersecting edges (connecting the midpoints
of the sides of a triangle that is one of the faces of a tetrahedron).
-
The height of a tetrahedron is a segment connecting a vertex with a point of the opposite face and perpendicular to this face
(it is a height drawn from any face and also coincides with the center of the circumscribed circle).
Additional Properties
-
All medians and bimedians of the tetrahedron intersect at one point.
-
This point divides the medians in a ratio of 3:1, counting from the vertex.
-
This point divides the bimedians in half.
Formulas for a Tetrahedron
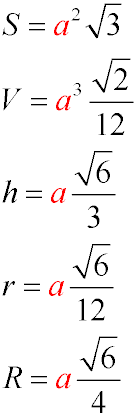
V - Volume Where a is the length of an edge.
S - Surface Area:
h - Height
r - Radius of the Inscribed Circle:
R - Radius of the Circumscribed Circle
With a triangle at the base |
Описание курса
| Regular tetrahedron
|

